という考え方を用いているのです。 平行四辺形の面積が (底辺)×(高さ) で求めれることを思い出してもらうと 三角形の面積公式は、このように考えることができますね。 三角形の面積を求めるためには 一旦、平行四辺形の面積を求め それを半分 正四角錐台の体積 のことなんじゃないかな。 プリンみたいな立体だよ。 正四角錐台は台形の立体バージョンにみえるし、たぶんそう。。 そこで今日は台形の体積のかわりに、 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。なので、 二等辺三角形の面積を求めて、それを8つ分にする。 という考え方で正八角形の面積を求めていきます。 中心の360°を8等分していることから 二等辺三角形の頂角は であることが分かりますね。 そして、次のように補助線を引くと 45°、45°、90

すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント
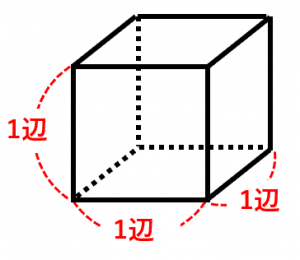
正方形の体積の求め方
正方形の体積の求め方-という方に向けて、 今回の記事では四角柱の体積・表面積の求め方について、 サクッと解説していきます(^^) 難しい説明などは省いて、問題を解けることを優先しております。 この記事を読みながら手元の宿題やワークを一緒に解き進めていきましょう。 本記事では、弓形の面積の求め方について説明します。 弓形の面積 図1 半径r、中心角θの弓形 弓形とは円とその割線(円と異なる二点で交わる直線)で囲まれる図形で、図1における網掛け部分のような図形です。実はその反対側も弓形です。



立方体と直方体の体積を計算する方法とツール 具体例で学ぶ数学
正多角形をすべての対角線で分けた二等辺三角形の面積を求めて、その和を求める方法もあるので、上記の公式を無理して覚える必要はありません。 (二等辺三角形に分ける方法については、計算問題①で解説します!) 正 n 角形の面積の公式(n = 3, 4, 5, 6)6年算数 円の面積1 子どもの学習支援 by いっちに算数 スマホ版 「円周率と円周と直径・半径」の勉強を忘れている時は、5年の「円と正多角形」でおさらいをしまょう。 「長方形・正方形の面積」の求め方を忘れている時は、4年の「面積」でおさらいをしましょう。扇形の面積を求める公式は、S = πr^2 × x/360 = 1/2 lr で表されます。このページでは、扇形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。
すべての辺の長さが2 cm である正四角錐oabcd において,辺oc 上に中点e をとる。この正四角錐の 側面上に,頂点a から辺ob と交わり点e まで線をひ くとき,最も短くなるようにひいた線の長さを求めな さい。 類題 2 1 辺が6cm の正方形abcd について,辺bc 平行四辺形の面積は、 「面積 底辺 高さ」 「 面 積 = 底 辺 × 高 さ 」 で求められます。 たとえば、「底辺 4 c m ,高さ 3 c m の平行四辺形」の面積は 4 × 3 = 12 c m 2 となります。 これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて 3 c m といっても、長方形や正方形の面積を求める公式は、知っている人も多いと思いますので、「そんなの知ってるよ」という人は、今日の記事は物足りないかもしれません。 まず、正方形の面積の公式は、 たて×よこ です。昨日、長方形の面積の求め方!
長方形の面積は,「たての長さ」×「横の長さ」で求められると考えてよいのでしょうか。 長方形の面積=たての「数」×横の「数」と考えます。 面積は,図形を敷き詰めた単位正方形のいくつ分かの数で表します。 単位正方形\(e\)正多角形の内角・外角の求め方を解説! 星形の角度の求め方を解説! ブーメラン型の角度の求め方! ちょうちょ型の角度の求め方を解説! 合同な図形の基本性質とは? 三角形の合同条件を使って、合同な三角形を見つける方法!・正三角形(面積から辺と高さ) 正三角形の面積から1辺の長さと高さを計算します。 直角三角形 ・直角三角形(底辺と高さ) 直角三角形の底辺と高さから、斜辺と角度と面積を計算します。




どうして1 3なの 錐の体積の公式の求め方 まなべーと




直方体 立方体の体積 Youtube
直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の 2本の対角線の長さ a, b と対角線の交わる角度 θ が分かっている場合、その四角形の面積 S は S = 1 2 a b sin θ で求められます。 関連記事 三角関数の基礎知識。 sinθ cosθ tanθ の覚え方・弧度法・三角比の表まとめ たとえば、「2本の対角線の長さが 8体積Vが8の立方体の1辺の長さ・表面積 1辺の長さ a:2 表面積 S:24 体積・表面積の計算 ・ 立方体の体積・表面積 ・ 立方体の体積から1辺 ・ 立方体の表面積から1辺 ・ 直方体の体積・表面積 ・ 直方体の1辺・表面積




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館




6年算数角柱と円柱の体積 立体の体積 教え方
正多角形の面積の公式 1辺の長さを a ~a~ a とした、正三角形から正六角形までの面積を求めます。 Ⅰ 面積の公式 Ⅱ 面積の公式の証明 Ⅰ 面積の公式 1辺 a ~a~ a の正四角形(正方形) と求まる。 三角比の値が、手計算でわかる n ~n~ n の値は、 n = 3, 4の体積 V = πr2h V = π r 2 h 体積 = 半径 × 半径 × 314 × 高さ 公式の 導出 ( どうしゅつ ) 方法と計算例は、「 円柱の体積の求め方 」をご覧ください。 円柱の体積の求め方 今回は小学校の算数で勉強する、円の面積・円周の求め方について書いていきたいと思います。(年6月日追記しました。) 円周の求め方公式 円の面積の求め方公式 円の面積・円周の長さを求める問題 問題① 《円の面積の求め方》 《円周の長さの求め方》 問題② 《円周



算数流体積の求め方 Sciencelab 冨田塾




すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント
円柱の体積の求め方 公式と計算例 Scipursuit 体積の求め方 円柱 円柱の体積を求める公式は、次の通りです。 V = Sh = πr2h V = S h = π r 2 h ここで、V は円柱の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の円の半径 対角線の長さが 10cmの正方形ABCDの面積を求めてください。 この面積の求め方はとっても簡単。 対角線を2回かけて、最後に2でわってやればいいんだ。 まとめ:正四角錐の体積の求め方も大丈夫! 正四角錐の体積の公式はどうだった? ? 底面積×高さ×1/3 という計算をゆっくりしてみてね。 テスト前に復習しておくと心強いかも! そんじゃねー Ken




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




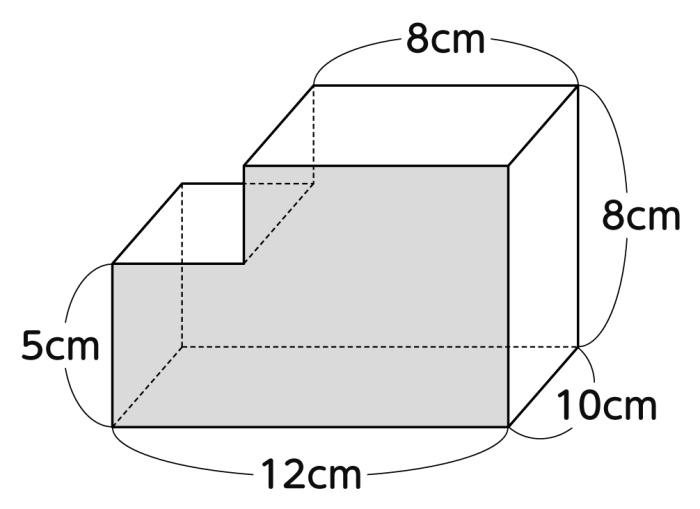
複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座
三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。 ここでは、三辺の長さが分かっている 場合 (ばあい) や、 角度 正方形の面積の求め方は? 長方形は「たて×よこ」、正方形は「一辺×一辺」で面積を求めることができます。 なぜ、このような公式で求めることができるのか考えてみましょう。 まずは、面積の基準についてみていきます。 面積の単位の基準である四角錐 ⇒ (上底下底)÷2×高さ×四角柱の高さ÷3 体積の求め方、覚え方 体積の公式の覚え方は簡単です。球の体積を除けば、たった2つの公式を覚えるだけで済むからです。



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
基本的には今まで説明した四角柱の体積と表面積の求めた方と同じですが、正六面体について説明します。 こちらはおまけ程度に確認してください。 立方体の体積 例えば、一辺が2cmの立方体の体積について考えてみましょう。



底面積とは 1分でわかる意味 求め方 円錐 三角錐 四角柱との関係 側面積との違い



動画で学習 1 角柱と円柱の体積 算数




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
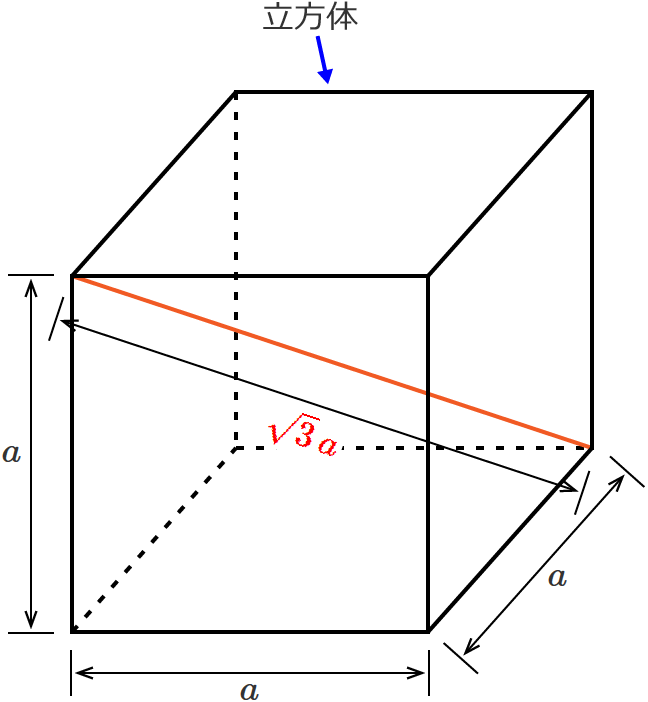



立方体の対角線の長さの求め方



算数科予習プリント 体積の求め方は考えられたかな 翁島 おきなしま 小学校ホームページ
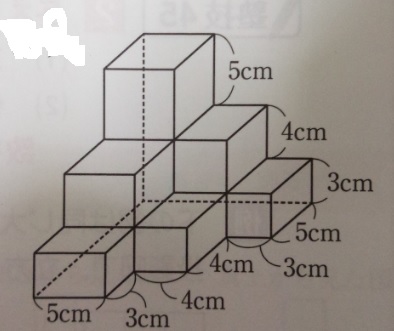



積み重ねられた立体 表面積と体積 中学受験 塾なし の勉強法



算数科予習プリント 水の体積はどうやって求めるのだろう 容積 って 何だろう 翁島 おきなしま 小学校ホームページ




どうして1 3なの 錐の体積の公式の求め方 まなべーと



地図の体積計測



立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学



3




体積の求め方 計算公式一覧



三角柱の体積の求め方




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー




くふうして体積を計算しよう 家庭学習レシピ




立方体の表面積を求める計算と公式 辺と表面積の対応表つき Irohabook
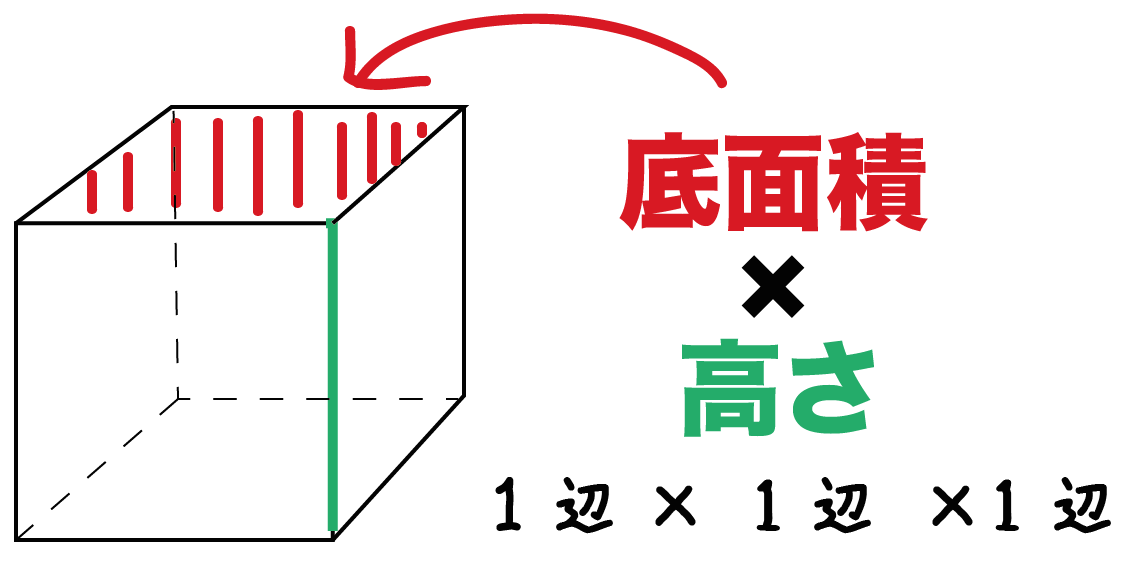



計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
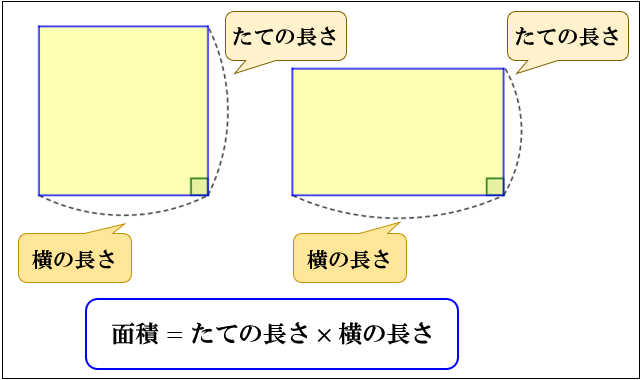



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
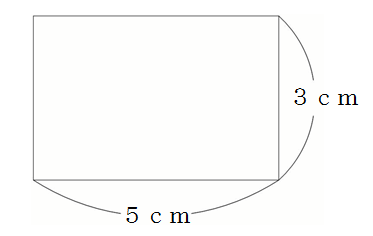



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




世界一分かりやすい算数 小5 体積



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書
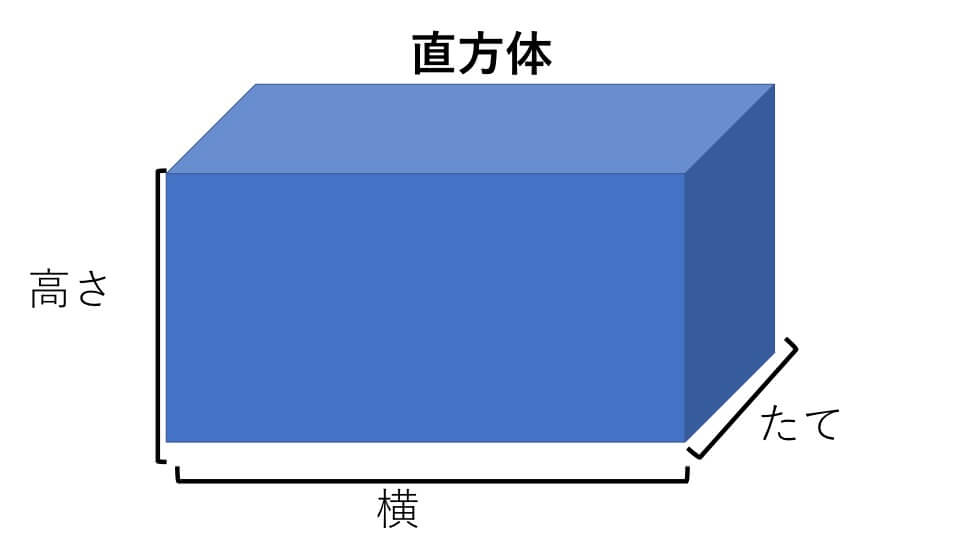



中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー



算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋



1




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




角柱の体積 Youtube



この立体の体積の求め方を分かりやすく説明つきで教えて下さい Yahoo 知恵袋
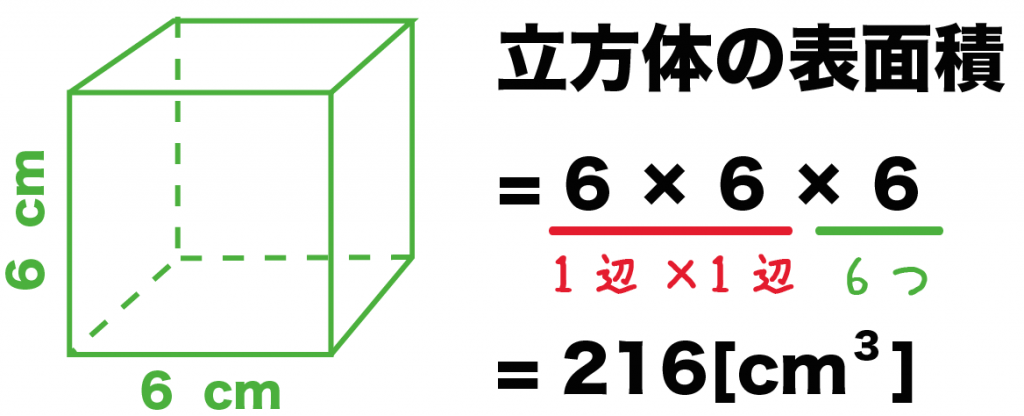



計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
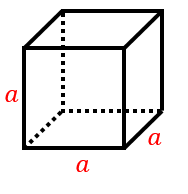



立方体と直方体の表面積を計算する 具体例で学ぶ数学
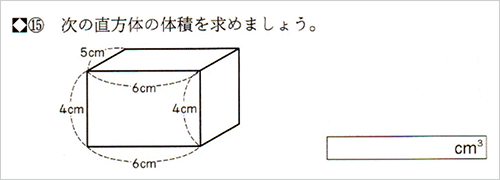



私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題
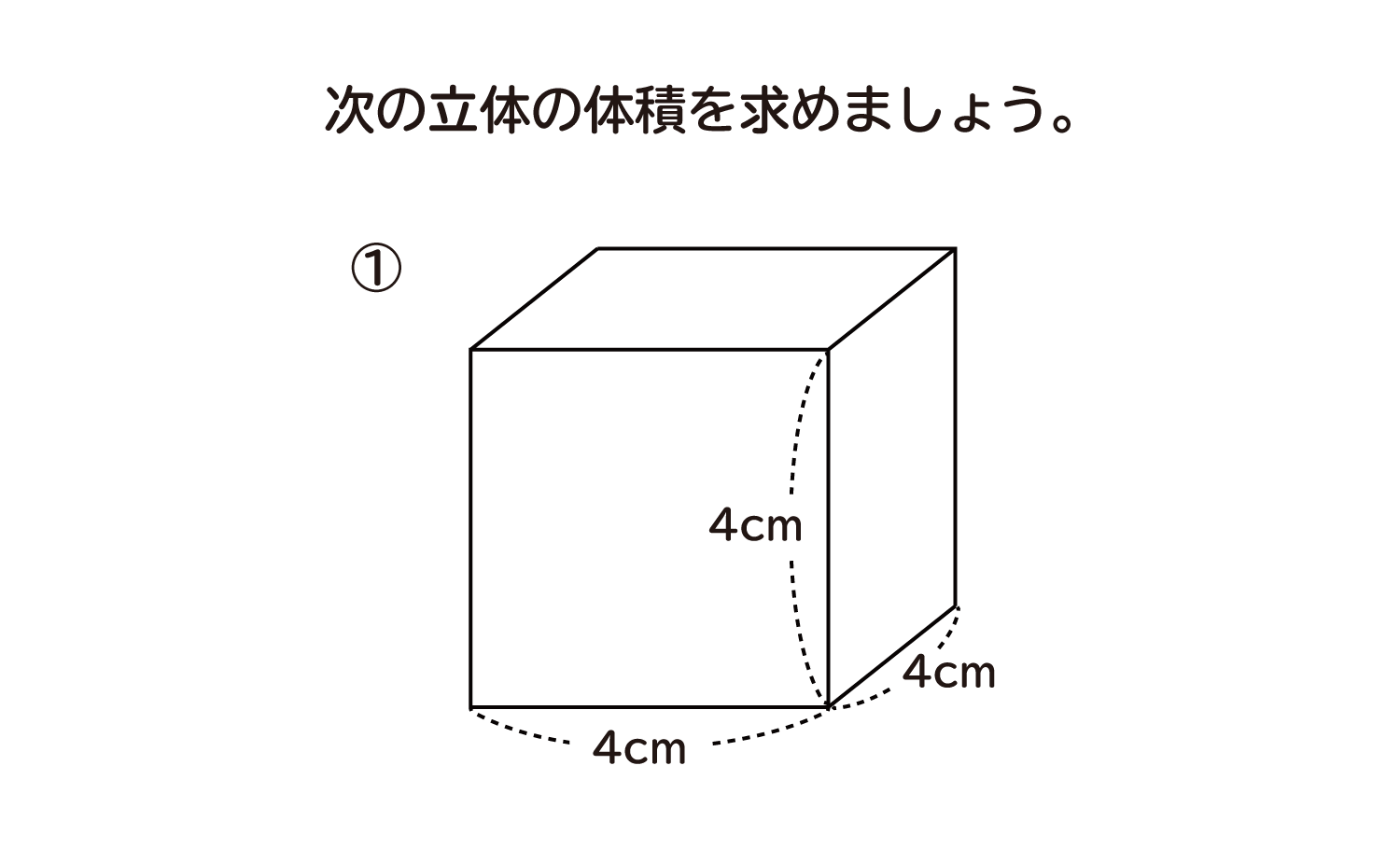



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
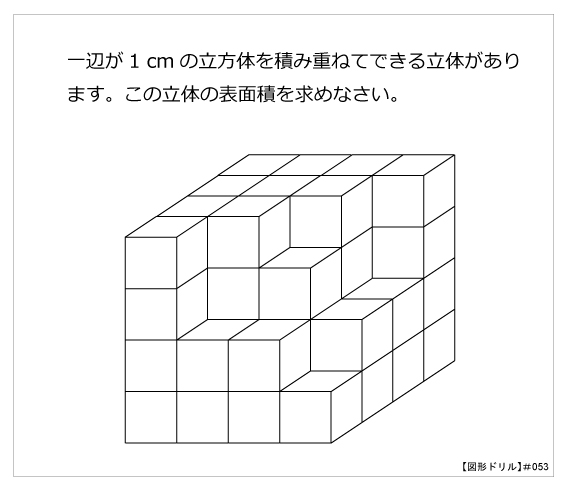



第53問 立方体と表面積 図形ドリル 第53問 立方体と表面積 算数星人のweb問題集 中学受験算数の問題に挑戦
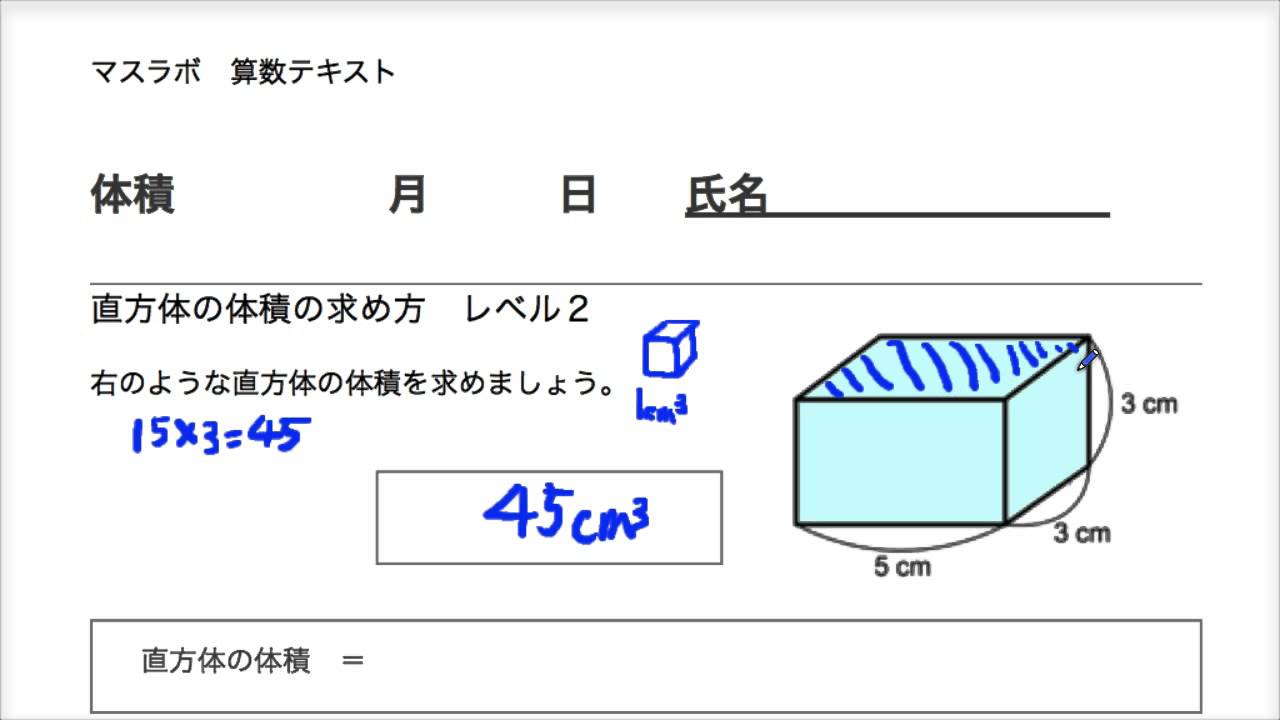



マスラボ 小学校5年 体積 レベル2 直方体の体積の求め方 Youtube
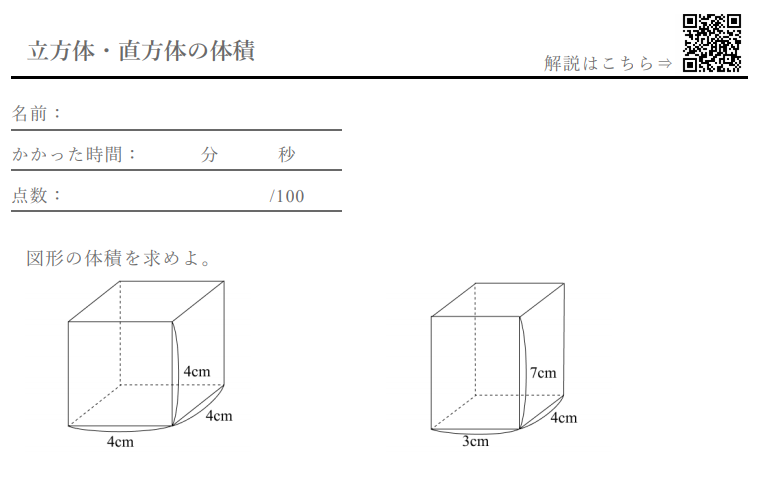



立方体 直方体 の体積 計算ドリル 問題集 数学fun
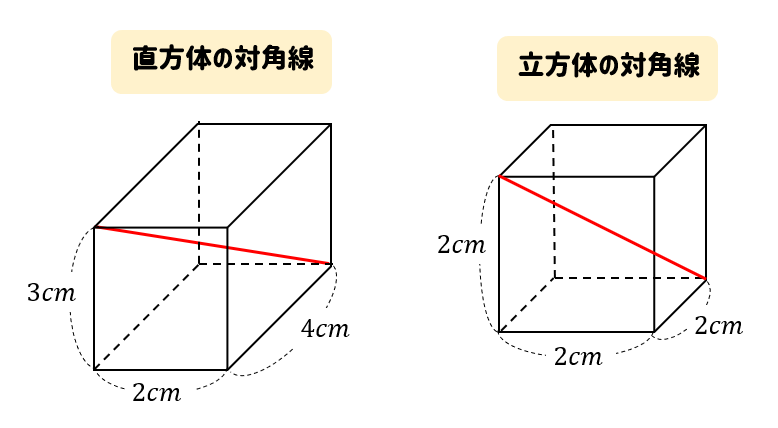



直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




マスラボ 小学校5年 体積 レベル3 立方体の体積の求め方 Youtube
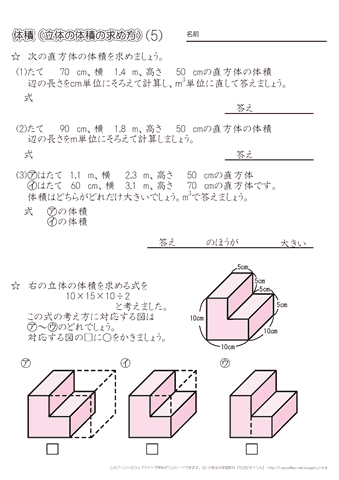



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




立方体と直方体の体積を計算する方法とツール 具体例で学ぶ数学
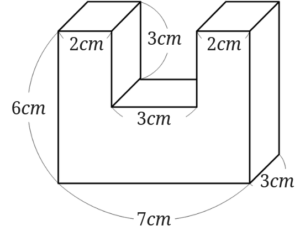



直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強



6年算数角柱と円柱の体積 立体の体積 教え方



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム
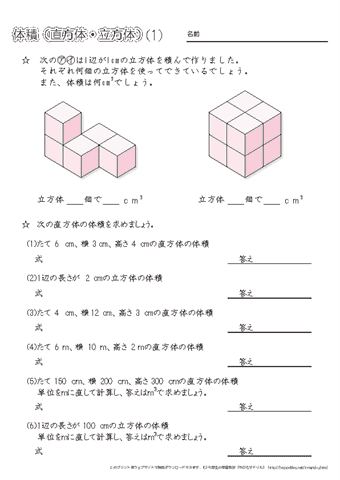



小学5年生の算数 体積 直方体と立方体の体積の求め方 練習プリント ちびむすドリル 小学生




体積 上 体積の意味から 立方体 直方体 柱 錐の体積の求め方 思考力算数練習張シリーズ 46 エム アクセス 本 通販 Amazon
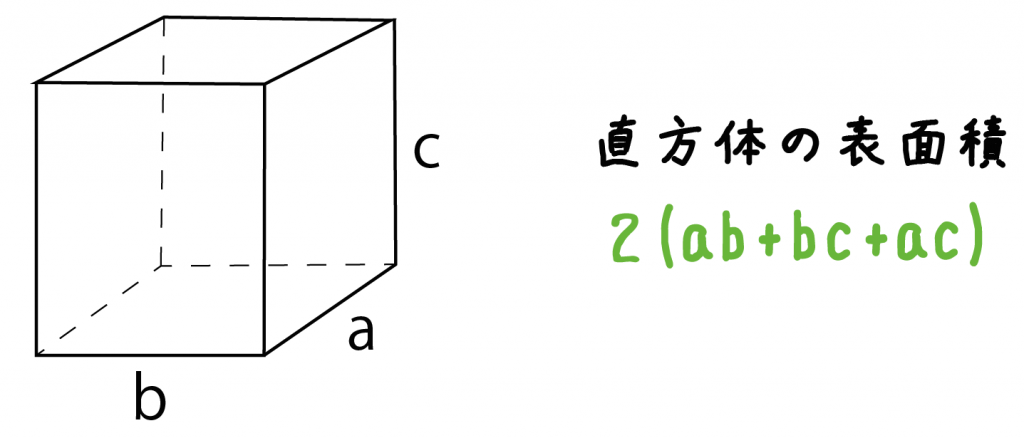



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



5年算数体積2わかる教え方
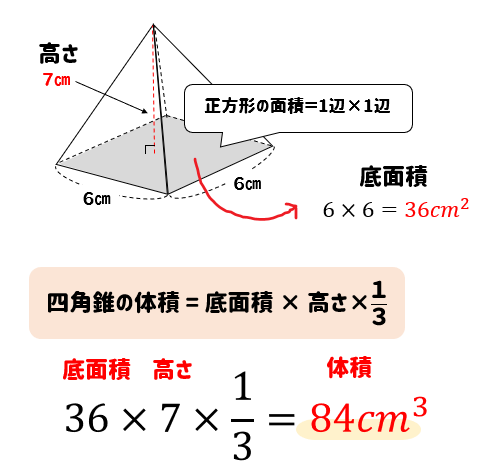



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ
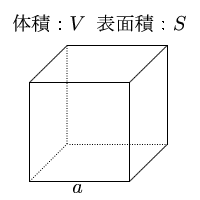



立方体の体積から1辺 体積 表面積の計算 計算サイト



四角柱の体積の公式は 1分でわかる求め方 公式と計算 表面積




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
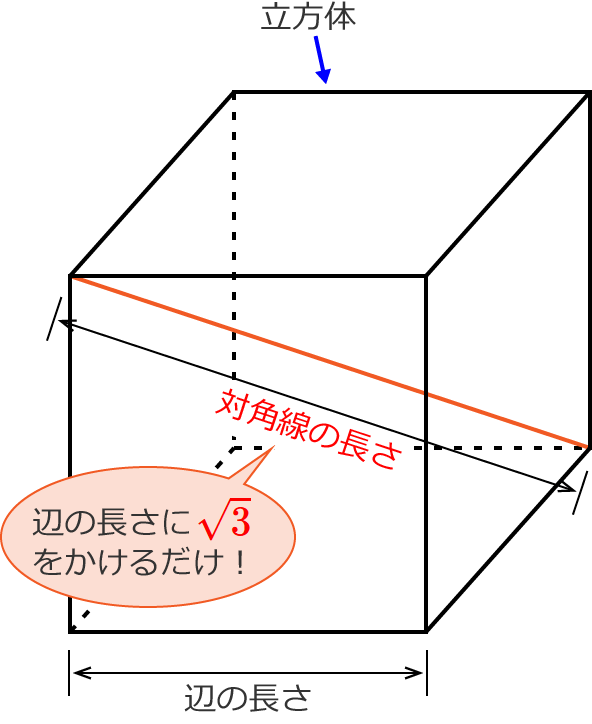



立方体の対角線の長さの求め方




小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生
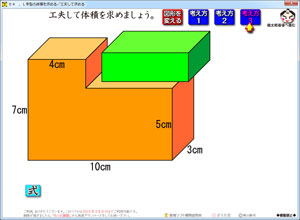



5年 算数ソフト 体積 さくら社




小学校5年 算数 大きな体積とかさ 台の形の体積 Youtube




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
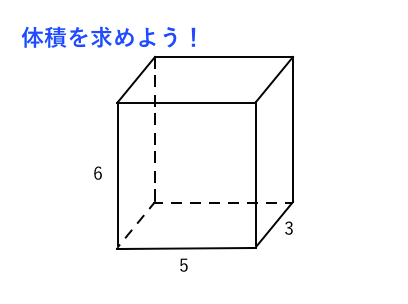



超簡単 体積の求め方 苦手な数学を簡単に




算数 新 小5編 体積 小4から始める高校受験 お母さん 一緒にがんばりましょう




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



兵庫県実践事例 算数小学校6年




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




体積 直方体 立方体 5 算数 算術 勉強方法



一辺が12cmの立方体の中にある三角錐の体積の求め方を教えてく Yahoo 知恵袋




表面積の求め方 計算公式一覧




立体の表面積 小学生算数です教えて下さい Okwave
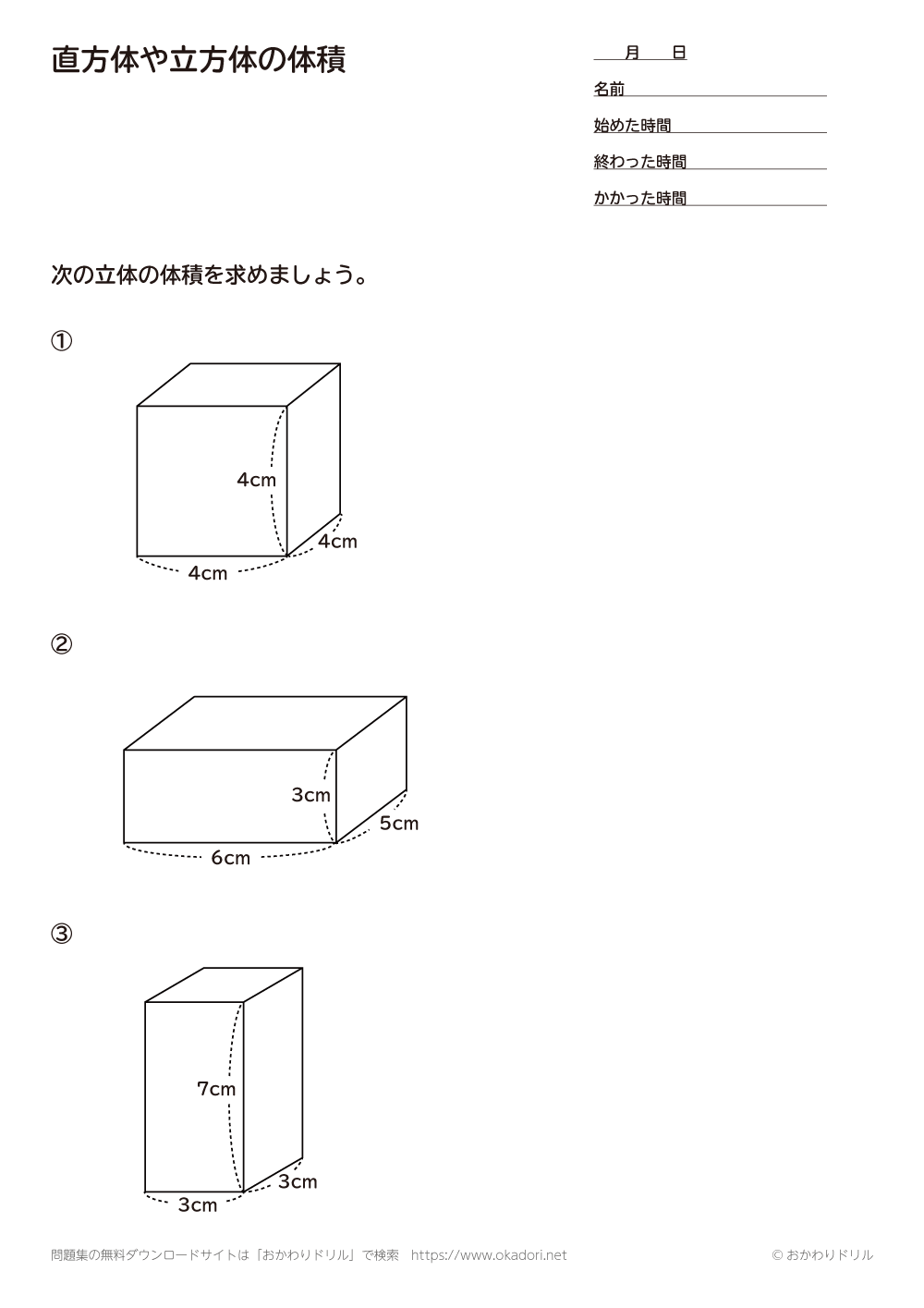



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




小5 算数 小5 3 直方体と立方体の体積 Youtube




四角柱の表面積を求める問題なんですが 側面積 底面積をしても答えの通りになり Clearnote




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun




体積 表面積



5年算数体積2わかる教え方
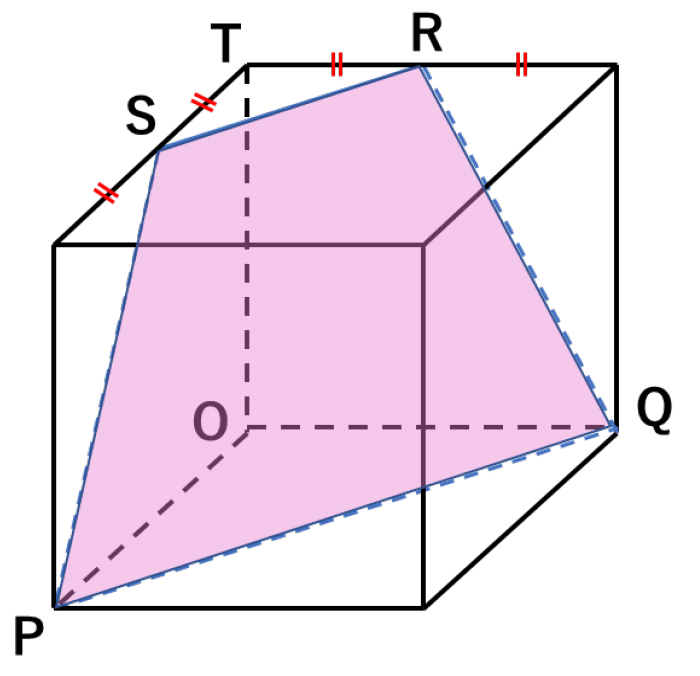



よく見かけますね この展開図 後編 中学受験プロ講師ブログ




計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



3



三角柱とは 体積 表面積の公式や求め方をわかりやすく解説 受験辞典




体積の求め方 立方体 長方体 小学生 算数のノート Clearnote



5年算数体積2わかる教え方



0 件のコメント:
コメントを投稿