A system of two linear inequalities is shown here { x 4 y ≥ 10 3 x − 2 y < 12 { x 4 y ≥ 10 3 x − 2 y < 12 To solve a system of linear inequalities, we will find values of the variables that are solutions to both inequalities We solve the system by using the graphs of each inequality and show the solution as a graphFor instance, the simple inequality x ≥ 3 denotes all real numbers x that are greater than or equal to 3 As with an equation, you solve an inequality in the variable x by finding all Graph y = x2 5x 12 You can see that the graph is above the xaxis when x is less than 4 or when x isWhereas to represent the inequality Y is greater than five on a number line and on the coordinate plane so let's do the number line first let me just draw out a number line that's my number line all the possible values of Y let's make that zero on the number line we could obviously go into the negative into negative numbers but we're going to be greater than five so I'll focus on the positive

Graph Inequality On Coordinate Plane Youtube
X y 1 graph the inequality on a plane
X y 1 graph the inequality on a plane-Graph the following inequalities (a) xy \leq 3 Graph the equation xy=3 first using the intercept method The intercepts occur at (3,0) and (0,3) The graph is a line passing through those points It is the boundary of the halfplane which represents the solution set of the given inequality Draw the line on the coordinate system We must now determine the ordered pairs which satisfy theTo solve your inequality using the Inequality Calculator, type in your inequality like x7>9 The inequality solver will then show you the steps to help you learn how to solve it on your own



Systems Of Linear Inequalities Solutions Of These Systems Pictures Examples And Practice Problems
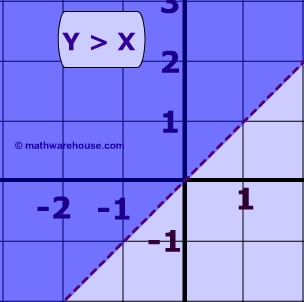
Start studying 103 Quiz Inequalities in Two Variables Learn vocabulary, terms, and more with flashcards, games, and other study toolsThe graph of y ≤ x The graph of y ≥ x Examine the 3 graphs below to understand how linear inqualities relate to a linear equation Below is the graph of the equation of the line y = x 1 The equation of y ≥ x 1 The equation of y ≤ x 1 The graph of y > x 1Solve linear, quadratic and absolute inequalities, stepbystep \square!
Now an inequality uses a greater than, less than symbol, and all that we have to do to graph an inequality is find the the number, '3' in this case and color in everything above or below it Just rememberGraphing Inequalities To graph an inequality, treat the , or ≥ sign as an = sign, and graph the equation If the inequality is < or >, graph the equation as a dotted lineIf the inequality is ≤ or ≥, graph the equation as a solid lineThis line divides the xy plane into two regions a region that satisfies the inequality, and a region that does not Steps on Graphing Linear Inequalities Step 1 Always start by isolating the variable y on the left side of the inequality Step 2 Change the inequality to equality symbol Step 3 Graph the boundary line from step 2 in the X Y − XY XY−plane Step 4 The last step is to shade one side or region of the boundary line
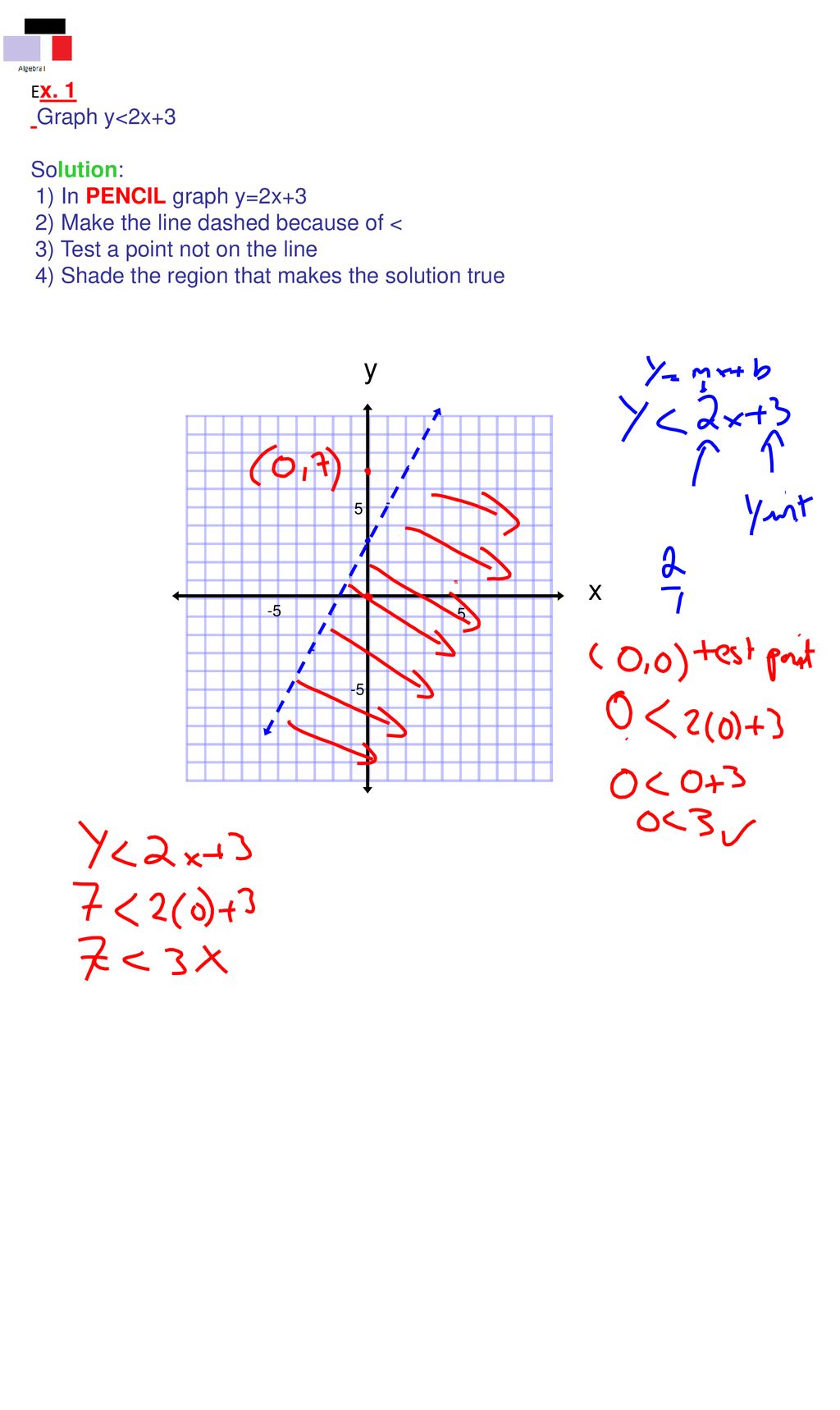
Graph the inequality y < 2x 2 Step 1 Graph the inequality as you would a linear equation Think of y = 2x 2 when you create the graph Remember to determine whether the line is solid or dotted In this case, since the inequality symbol is less than (👉 Learn how to graph linear inequalities written in standard form Linear inequalities are graphed the same way as linear equations, the only difference bei7 Shade The Appropriate Region Of The Graph, Based On The Inequality Sign To shade the appropriate region, we shade above or below the curve depending on the sign of the inequality For y > f(x) > 0 or y >= f(x), we shade above the parabola curve For y < f(x) or y




Which Of The Pictures Below Shows The Graph Of The Inequality Y X 2 Brainly Com



5 5 Linear Inequalities A Linear Inequality Describes The Region Of The Coordinate Plane That Has A Boundary Line Every Point In The Region Is A Solution Ppt Download
For example, this graph shows the inequality \(x \textless 1\) This can be seen as there is a dashed line at \(x = 1\) , and the region where the \(x\) coordinates are less than 1 is shadedExample 5 Graph the inequality y x≥ 3 6 Solution We first write the inequality as an equation, y x= 3 6 The line will be graphed as a solid line because the inequality in this problem is ≥, which includes the line We can graph the line using x and yintercepts, or by using the slope and yintercept from slopeintercept formGraph the solution set y > − 3 x 1 Solution Step 1 Graph the boundary Because of the strict inequality, we will graph the boundary y = − 3 x 1 using a dashed line We can see that the slope is m = − 3 = − 3 1 = r i s e r u n and the y intercept is (0, 1)




Example 1 Graph A Quadratic Inequality Graph Y X 2 3x 4 Solution Step 1 Graph Y X 2 3x 4 Because The Inequality Symbol Is Make The Parabola Ppt Download




Practice B Linear Inequalities In Two Variables Weeblyasb Bangna Practice B Linear Inequalities In Two Variables Graph Each Inequality 1 Y X 2 2 Y 3x 5 X Y X Y Solve Each Inequality
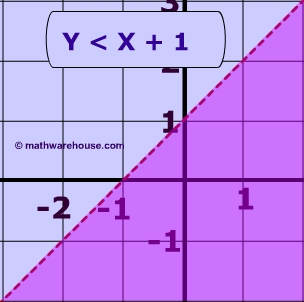
Write an inequality to describe the graph The dotted line has a slope of − 1 2 \frac {1} {2} − 2 1 and and a y y y intercept of 1, so the equation of the line is y = − 1 2 x 1 y=\frac {1} {2}x1 y = − 2 1 x 1 The line is dotted, so the solution set does not include the values on on the line Graphing an Inequality Solve the equation for y (if necessary) Graph the equation as if it contained an = sign Draw the line solid if the inequality is ≤ or ≥ Draw the line dashed if the inequality is < or > Pick a point not on the line to use as a test point The point (0,0) is a good test point if it is not on the lineWe dash the line if the values on the line are not included in the boundary If the values are included we draw a solid line as before Second we test a point in each region If one point on one side of the line satisfies our inequality, the
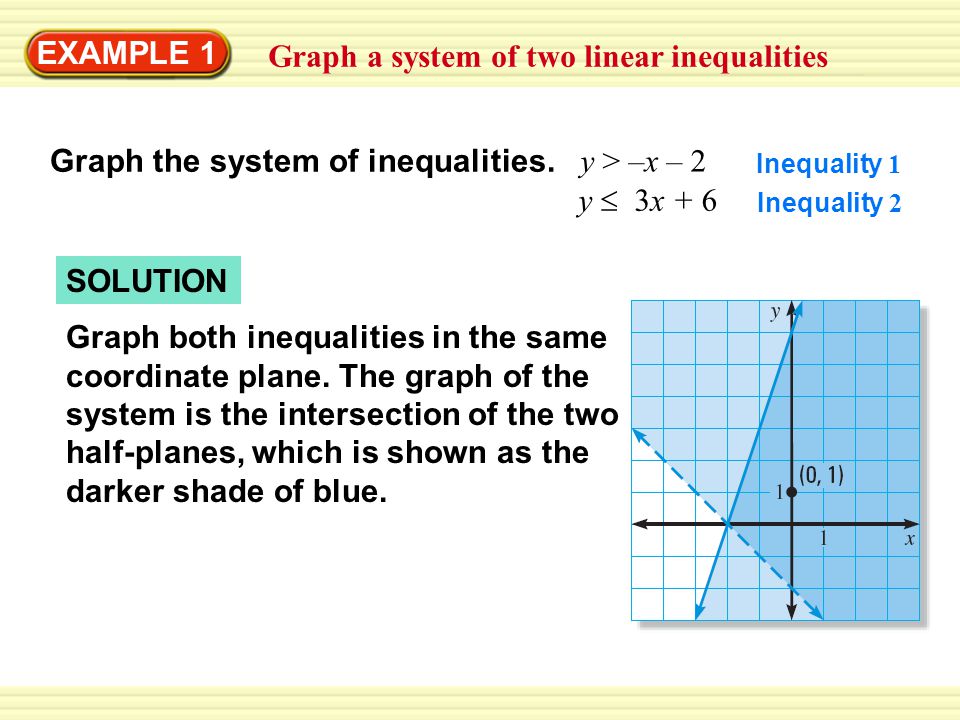



Solution Example 1 Graph A System Of Two Linear Inequalities Graph The System Of Inequalities Y X 2 Y 3x 6 Inequality 1 Inequality 2 Graph Both Ppt Download




How To Graph Linear Inequalities Krista King Math Online Math Tutor
2 Graph the inequality 4(x y) – 5(2x y) < 6 and answer the questions below a Check whether the point (22, 10) is within the solution set b Determine the slope of the border line 3 Graph the inequality of y< 3x and determine which quadrant will be completely shaded 4 Graph the inequality y > 3x 1 and answer the questions below aBelow is the graph of the inequality y > x 1 Step 1 The inequality is already in the form that we want That is, the variable y is isolated on the left side of the inequality Step 2 Change inequality to equality Therefore, y > x 1 becomes y = x 1 Step 3 Now graph the y = x 1Use the method that you prefer when graphing a lineView 27__HW_TwoVariable_Inequalities (1)pdf from MATH 361 at Robert E Lee High SChool Name 27 Class Date Practice Form G TwoVariable Inequalities Graph each inequality 1 y < x 5 x 2 2 y




Solve The Inequality X 2 1 Geq 0 By Reading The Corresponding Graph Y X 2 1 The Solution Set Is Type Your Answer In Interval Notation Use Integers Or Fractions



Linear Inequalities How To Graph The Equation Of A Linear Inequality
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Graphing Systems of Linear Inequalities To graph a linear inequality in two variables (say, x and y ), first get y alone on one side Then consider the related equation obtained by changing the inequality sign to an equality sign The graph of this equation is a line If the inequality is strict ( < or > ), graph a dashed lineThe graph you create will look like the graph i showed you except you would have shaded the area below the line to indicate that is where the solution to the inequality lies unlike an equality solution, the inequality solution will contain many values of y that are less than the value of x/3




Linear Inequalities Worksheet Linear Inequalities Graphing Linear Inequalities Graphing Inequalities
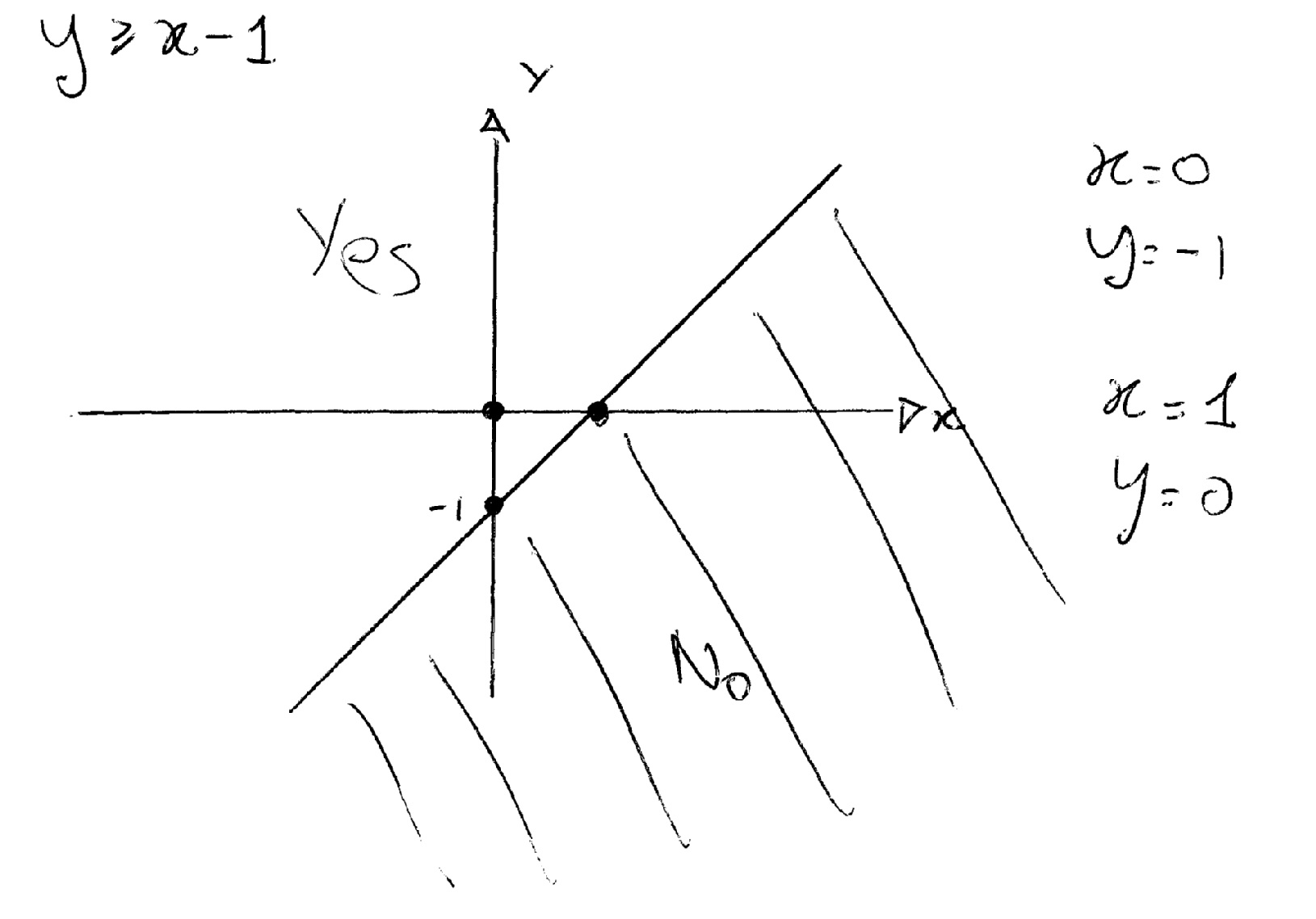



How Do You Graph The Inequality Y X 1 Socratic
First rearrange the inequality (if necessary) in the form Y < (or , >) f (X) Use the Y=f (X) command on the Generate menu to plot the boundary of the inequality If the inequality is < or > rather than < or >, the usual practice is to plot this boundary using a dashed line To change the line type of the boundary line or curve, right clickLearn how to graph the linear equation of a straight line y = x using table methodThe graph of the inequality y > x 4 y > x 4 is shown in Figure 434 below The line y = x 4 y = x 4 divides the plane into two regions The shaded side shows the solutions to the inequality y > x 4 y > x 4 The points on the boundary line, those where y = x 4 y = x 4, are not solutions to the inequality y > x 4 y > x 4, so




Solved Which Region In The Graph Below Is The Solution Of Chegg Com




Kelvin S Online Maths Absolute Values
Graphing Linear Inequalities This is a graph of a linear inequality The inequality y ≤ x 2 You can see the y = x 2 line, and the shaded area is where y is less than or equal to x 2Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high Transcribed image text Graph the inequality y > (x 1) (x 3) L 10 Graph Layers « 9 8 7 After you add an object to the graph you can use Graph Layers to view and edit its properties 6 5 Fill 4 3 v 2 1Graphing Inequalities To graph an inequality o Graph the related boundary line Replace the , ≤ or ≥ sign in the inequality with = to find the equation of the boundary line o Identify at least one ordered pair on either side of the boundary line and substitute those (x, y) values into the inequality
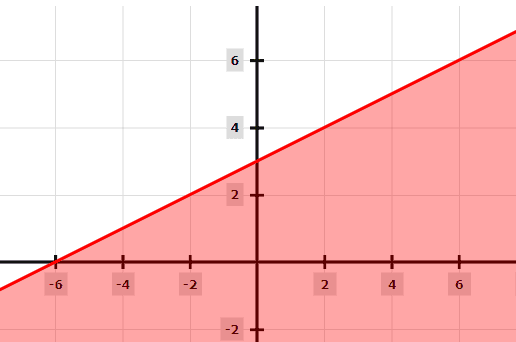



Graphing Linear Inequalities Explanation Examples




Which Graph Represents This System Of Inequalities Y Gt X 3 Y 5x 1 Brainly Com
Graphinequalitycom offers usable info on inequalities, greatest common factor and adding fractions and other math subjects Should you have to have help on solution as well as point, Graphinequalitycom is simply the right destination to explore!Graph xy>4 Solve for Tap for more steps Subtract from both sides of the inequality Multiply each term in by Tap for more steps Multiply each term in by When multiplying or dividing both sides of an inequality by a negative value, flip the direction of the inequality signGraph the inequality y < x Solution Replace the inequality symbol with an equal sign and graph the related equation y = x Plot two points to determine the line We can plot the points (0, 0) and (1, 1) Since the inequality symbol is
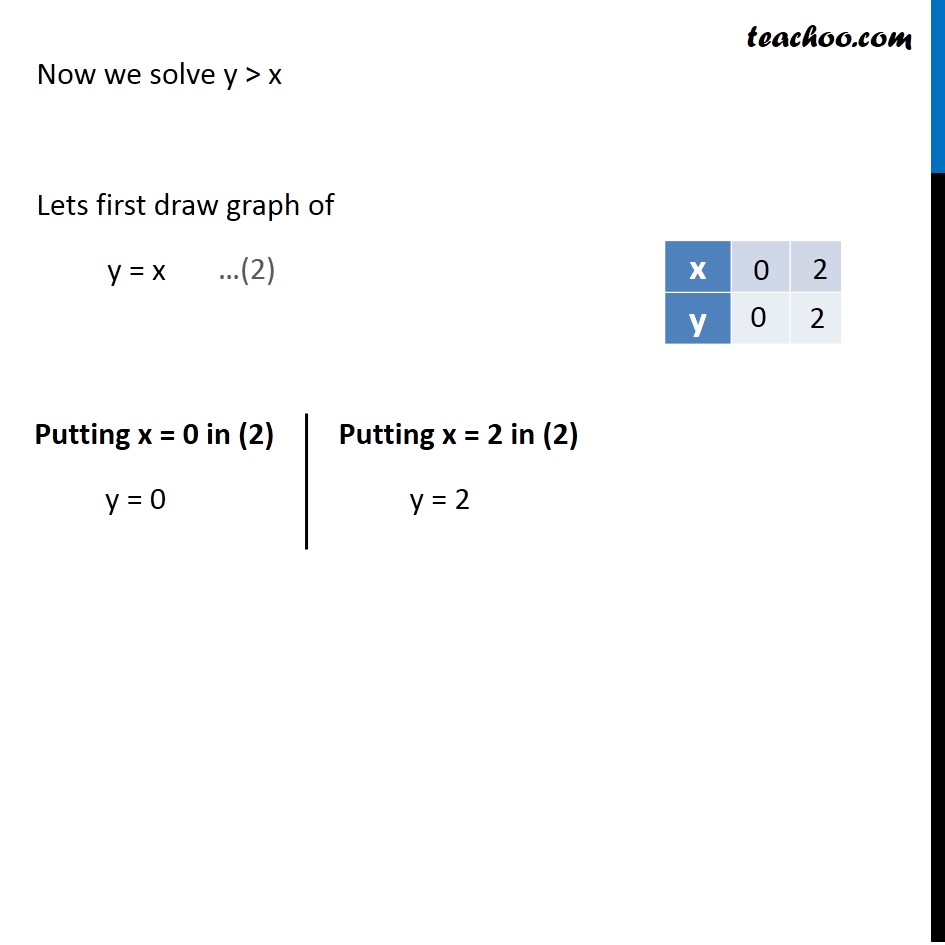



Ex 6 3 8 Solve X Y 9 Y X X 0 Graphically Ex 6 3




Systems Of Linear Inequalities Solutions Of These Systems Pictures Examples And Practice Problems
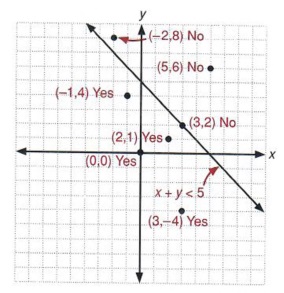
Graph inequalities In order to graph an inequality we work in 3 steps First we graph our boundaries; Linear inequalities are the expressions where any two values are compared by the inequality symbols such as, '', '≤' or '≥' These values could be numerical or algebraic or a combination of both For example, 1017 are examples of numerical inequalities and x>y, y 11 are the examples of algebraicExample By shading the unwanted region, show the region represented by the inequality x y < 1 Solution Rewrite the equation x y = 1in the form y = mx c x y = 1 can be written as y = –x 1 The gradient is then –1 and the yintercept is 1 We need to draw a dotted line because the inequality is < After drawing the dotted line, we need to shade the unwanted region



Graphing Linear Inequalities



How Do You Graph The System Of Inequalities X 0 Y 0 X Y 2 0 Socratic
Graphing Quadratic Inequalities A quadratic inequality of the form y > a x 2 b x c (or substitute < , ≥ or ≤ for > ) represents a region of the plane bounded by a parabola To graph a quadratic inequality, start by graphing the parabola Then fill in the region either above or below it, depending on the inequalityTap for more steps Find the values of m m and b b using the form y = m x b y = m x b The slope of the line is the value of m m, and the yintercept is the value of b b Graph a dashed line, then shade the area below the boundary line since y y is less than 1 − x 1 x Graph x−y > 2 x yInsert the x and yvalues into the inequality x y ≥ 1 and see which ordered pair results in a true statement Since (4, 1) results in a true statement, the region that includes (4, 1) should be shaded Do the same with the second inequality Graph the boundary line, then test points to find which region is the solution to the inequality
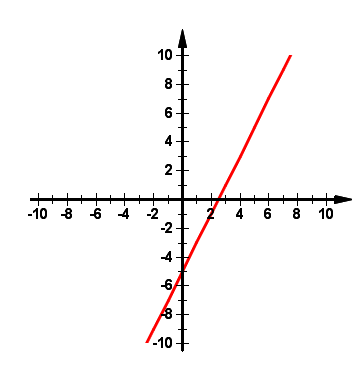



Dplot Graphing Inequalities



Graphing Inequalities On A Number Line
For instance, look at the top number line x = 3 We just put a little dot where the '3' is, right? y = 1 or (4,1) We can now graph the two points on the coordinate plane and draw a line through the points to mark the boundary of the inequality graph { (x^2 (y3)^035) ( (x4)^2 (y1)^035) (yx3)=0 10, 10, 5, 5} Now, we can shade the right side of the line We also need to change the boundary line to a dashed line because the If x is the number of hardcover books Tula can buy and y is the number of paperback books she can buy, the inequality models the situation ⓐ Graph the inequality ⓑ List three solutions to the inequality where both x and y are whole numbers




Graphing Linear Inequalities




Graphing Inequalities X Y Plane Review Article Khan Academy
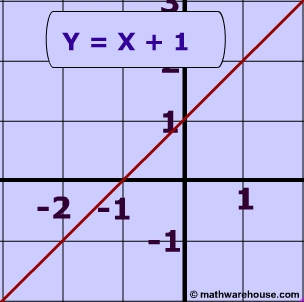



Linear Inequalities How To Graph The Equation Of A Linear Inequality




Desmos Graph Of Y Ln X And Y X 1 Download Scientific Diagram
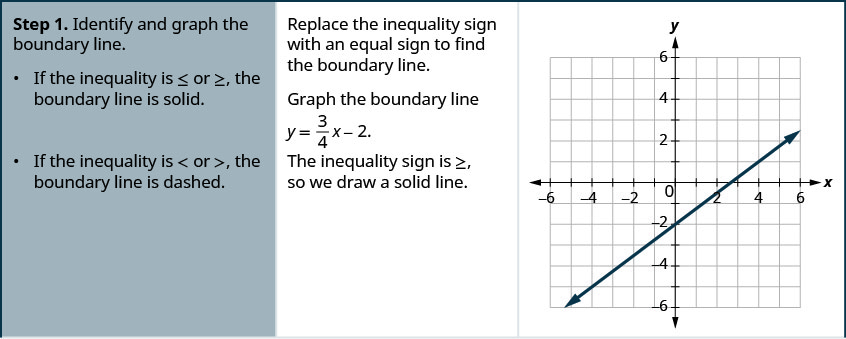



4 1 Graphing Linear Inequalities In Two Variables Mathematics Libretexts
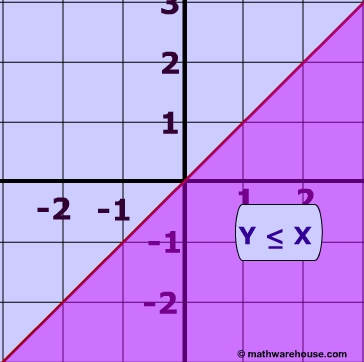



Linear Inequalities How To Graph The Equation Of A Linear Inequality
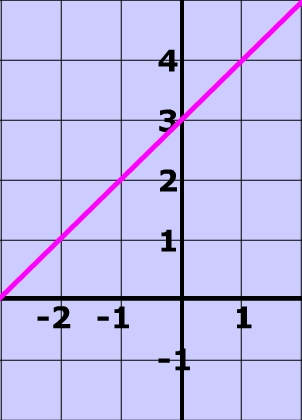



Linear Inequalities How To Graph The Equation Of A Linear Inequality
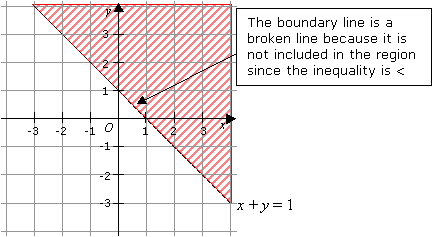



Graphing Inequalities Solutions Examples Videos
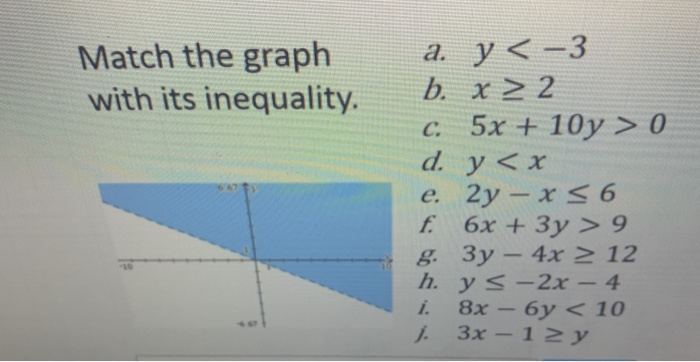



Solved Match The Graph With Its Inequality A Y 3 B X Chegg Com
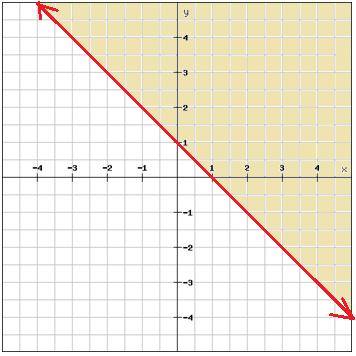



Linear Inequalities In Two Variables Algebra 1 Linear Inequalitites Mathplanet




3 5 Graph Linear Inequalities In Two Variables Mathematics Libretexts
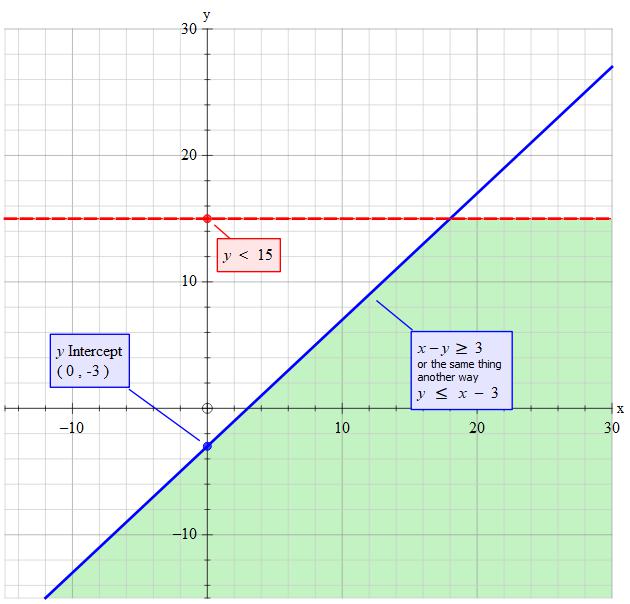



How Do You Graph The System Of Linear Inequalities X Y 3 And Y 15 Socratic
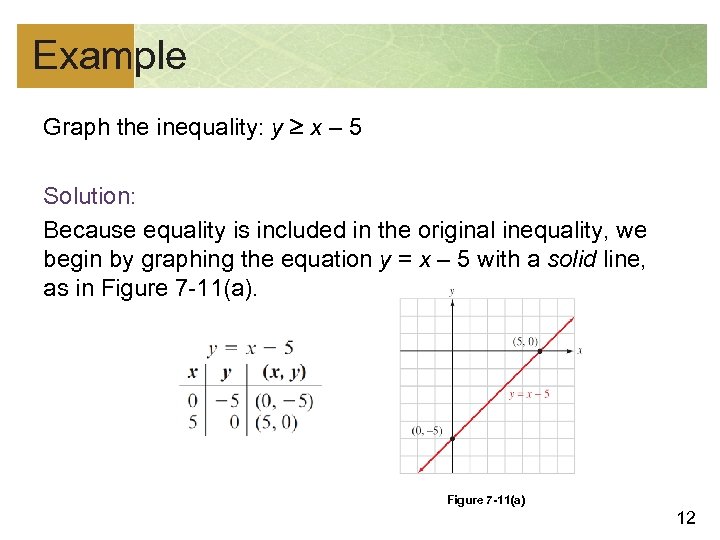



Systems Of Linear Equations And Inequalities In Two




Find The Graph Of The Inequality Y X 1 Help Brainly Com
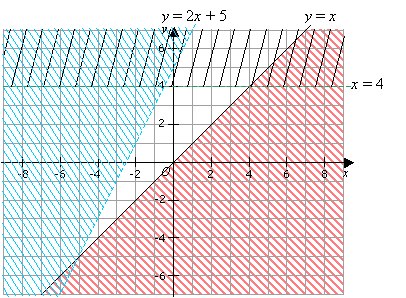



Graphing Inequalities Solutions Examples Videos
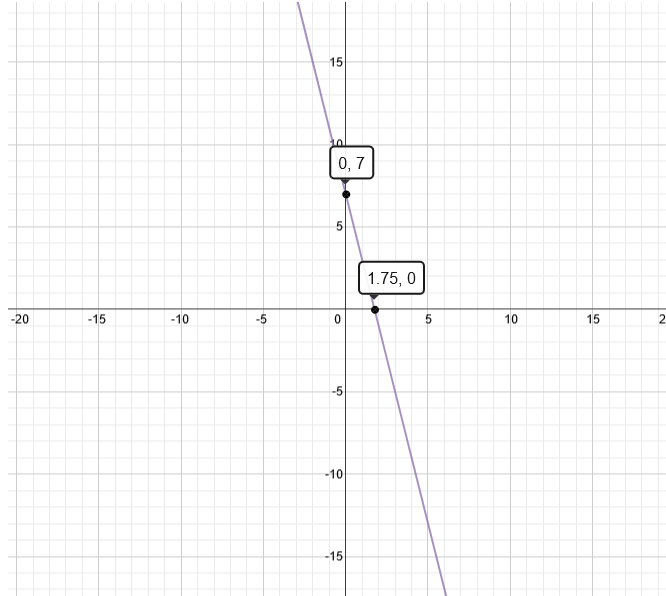



3 7 On A Graph Spg Pack Com




Mfg Linear Inequalities




Homework Help Graphing Inequalities What Is An Example Of An Inequality In Math
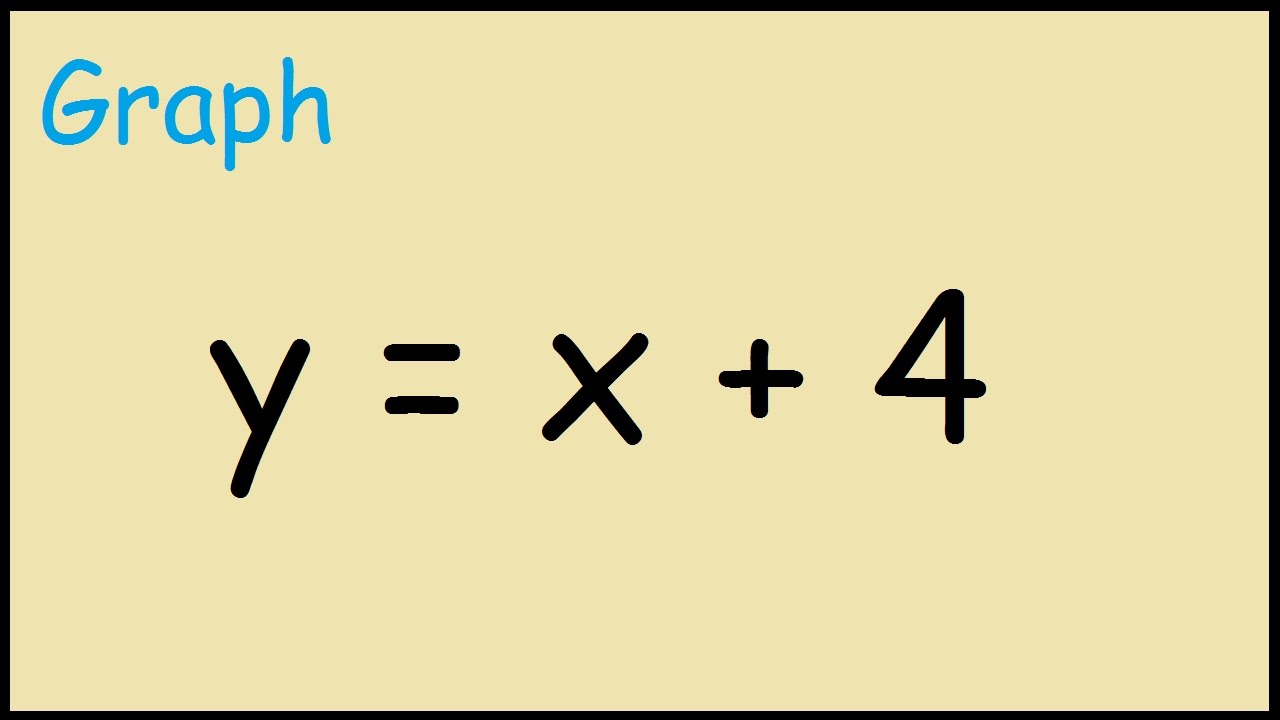



How To Graph Y X 4 Youtube




Lesson Worksheet Two Variable Absolute Value Inequalities Nagwa
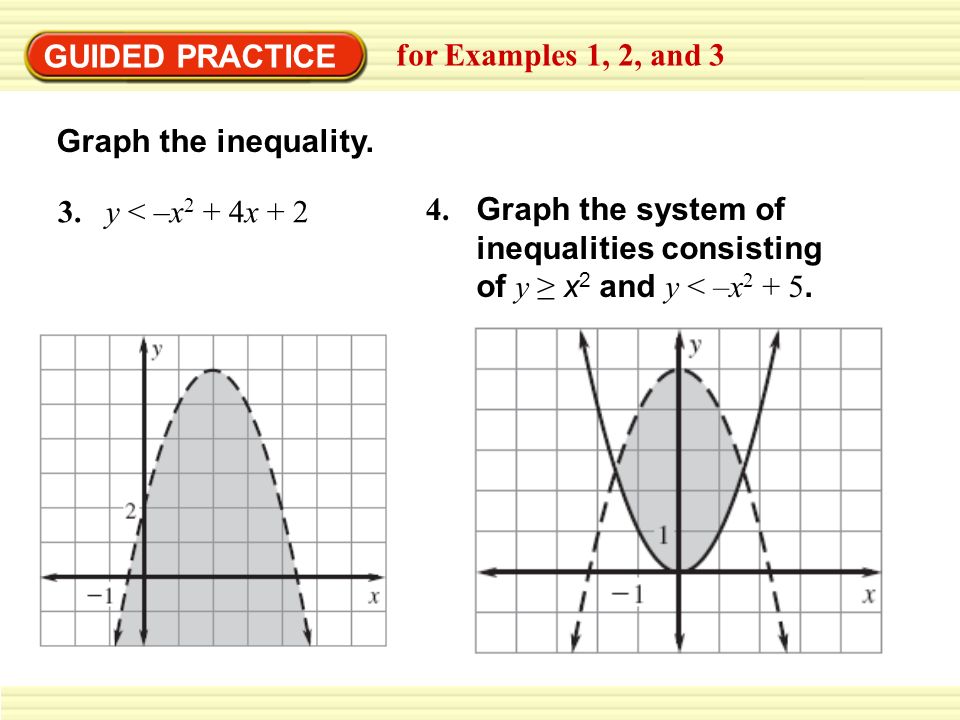



Example 1 Graph A Quadratic Inequality Graph Y X 2 3x 4 Solution Step 1 Graph Y X 2 3x 4 Because The Inequality Symbol Is Make The Parabola Ppt Download



Graphing Linear Inequalities Kate S Math Lessons
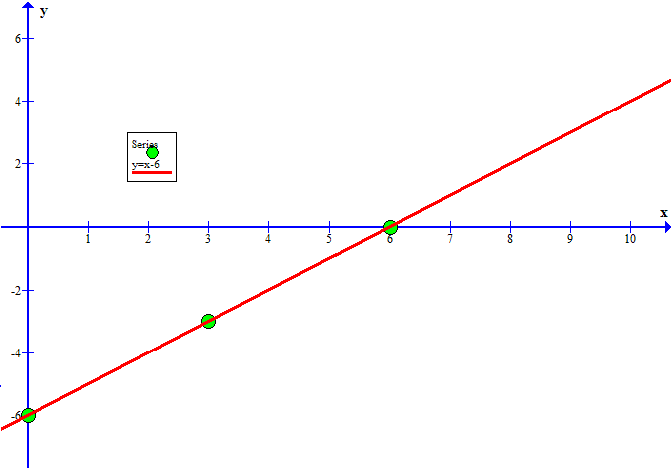



How Do You Graph The Inequality Y X 6 Socratic
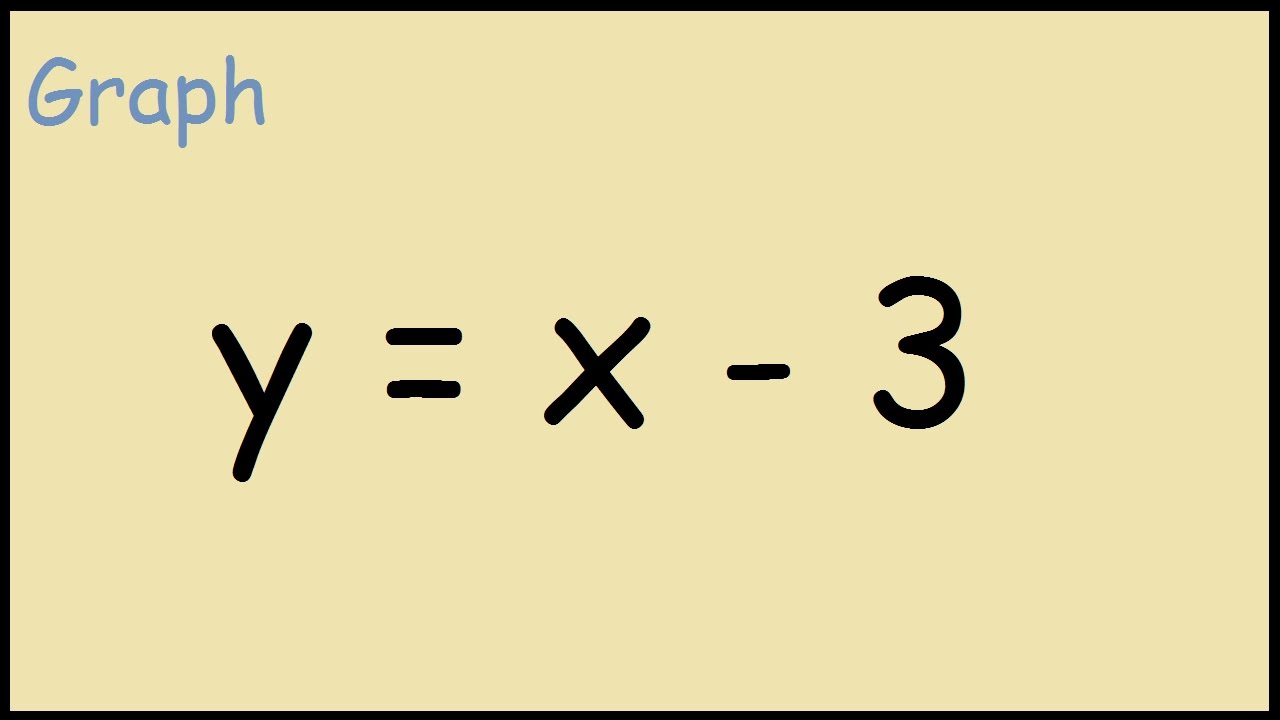



How To Graph Y X 3 Youtube
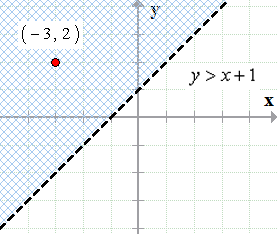



Graphing Linear Inequalities Chilimath




Solved L X Y X The Graph Of A Linear Inequality The Region Chegg Com
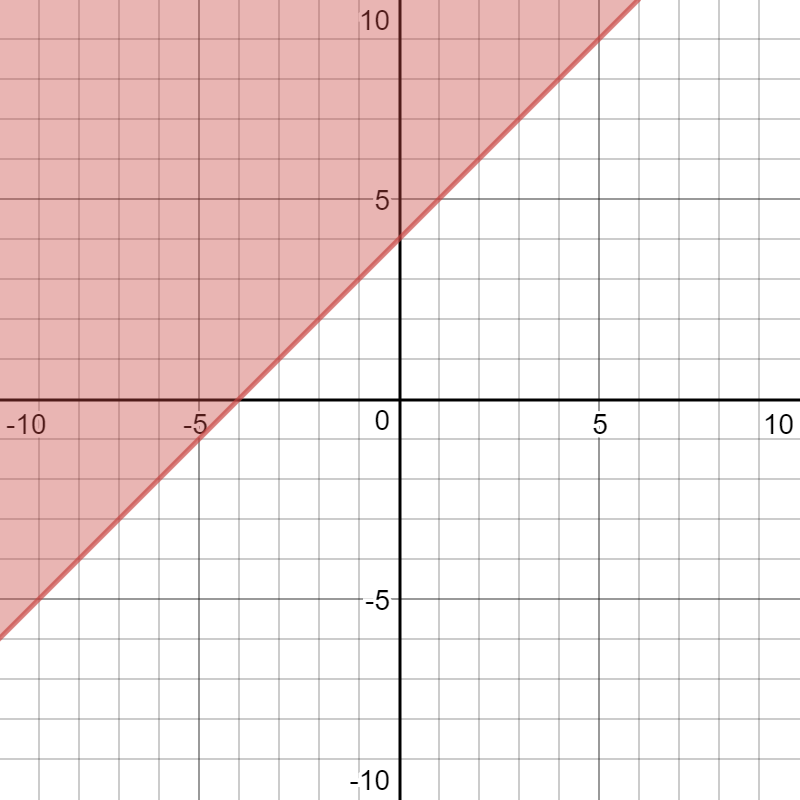



How Do You Graph The Inequality Y X 4 And Y 6x 3 Socratic
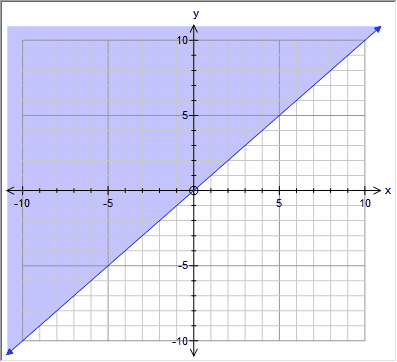



Graph Other Preferences
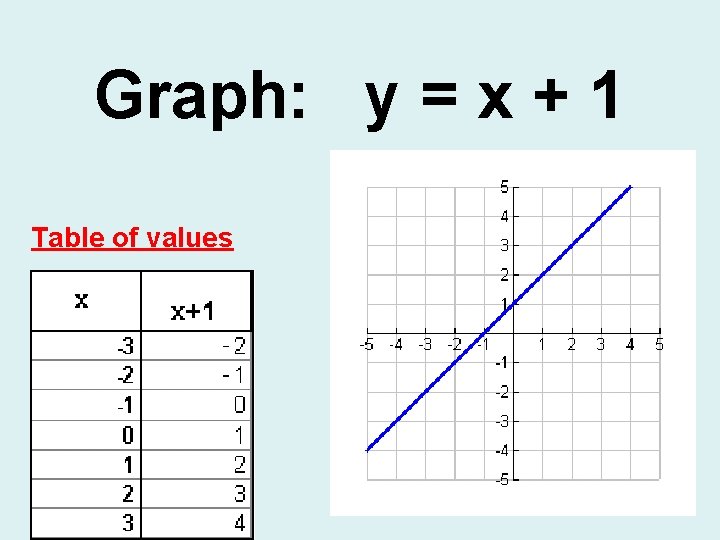



Graph The Linear Equation Yx 2 1 Draw




Graphing Linear Inequalities In Two Variables Lesson Essential
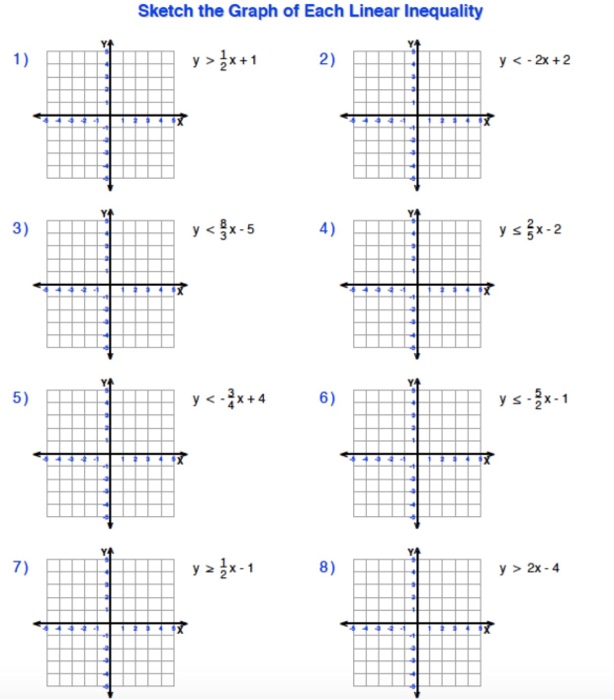



Solved Sketch The Graph Of Each Linear Inequality 1 Y X 1 Chegg Com



Inequalities Graphing Inequalities Sparknotes



Solution Graph The Following Inequality Y X Gt 3



Graphing Linear Inequalities With Python Programming Tips For Versatile Coders



Graph Graph Inequalities With Step By Step Math Problem Solver
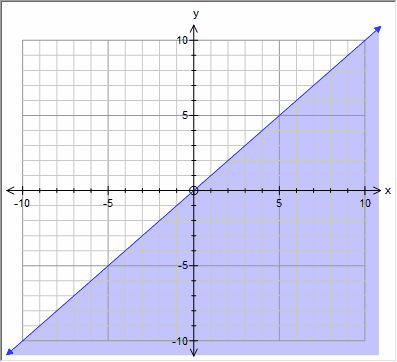



Graph Other Preferences



3
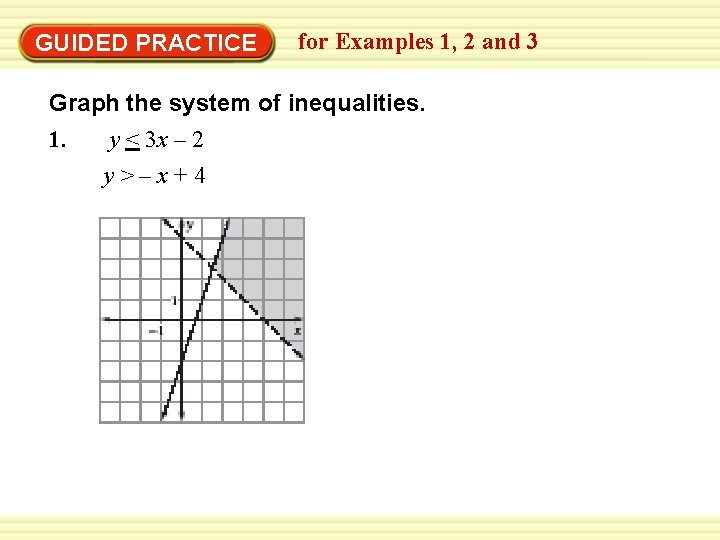



Example 1 Graph A System Of Two Inequalities




01 Graphing Inequalities In Two Variables Part 1 Solve Graph Shade Inequalities Youtube



How Do You Graph The Inequality X Y 4 Socratic
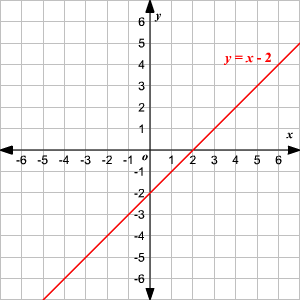



Graphing Systems Of Linear Inequalities
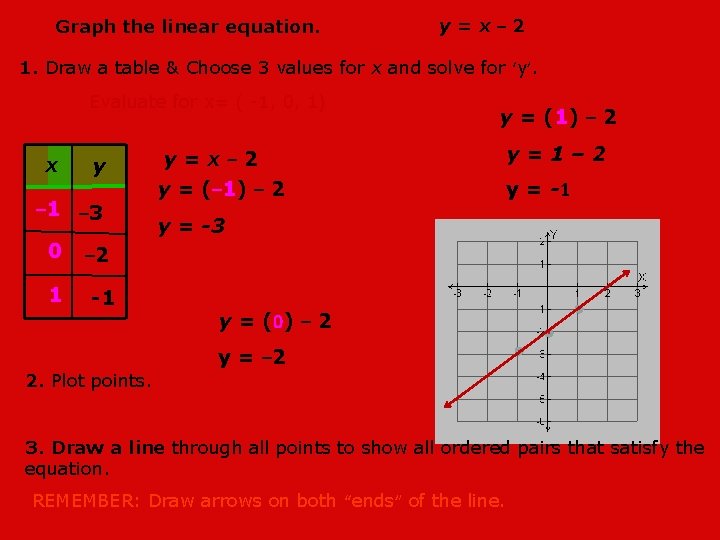



Graph The Linear Equation Yx 2 1 Draw




Graph Inequality On Coordinate Plane Youtube




Which Graph Represents The Solution Set Of The System Of Inequalities X Y Lt 12 Y X 4 Brainly Com




Systems Of Inequalities



Example 1 Graph A Quadratic Inequality Graph Y
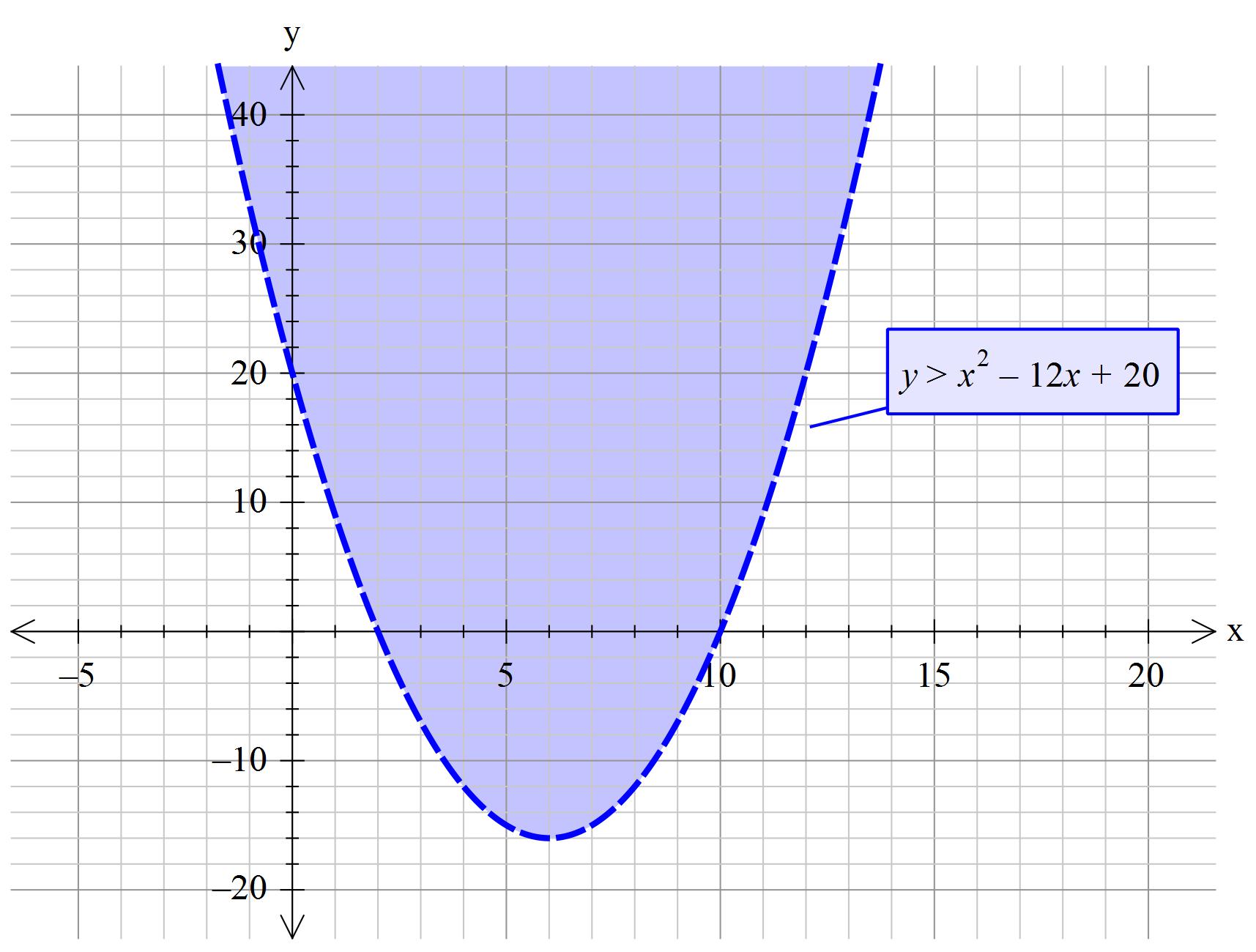



How Do You Graph The Inequality X 2 12x 32 12 Socratic




Which System Of Linear Inequalities Is Represented By The Graph O Y Gt X 2 And Y Lt X 1 O Y X Brainly Com




Graphing Inequalities X Y Plane Review Article Khan Academy




Graphing Linear Inequalities



Graphing Linear Inequalities




Graph The Inequalities Y X 4



Inequalities Graphing Inequalities Sparknotes




Graph The Linear Inequality Y X Study Com
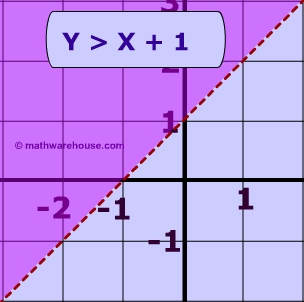



Linear Inequalities How To Graph The Equation Of A Linear Inequality



1




Graph Inequality On Coordinate Plane Youtube



1




Graphing Linear Inequalities In Two Variables Lesson Essential
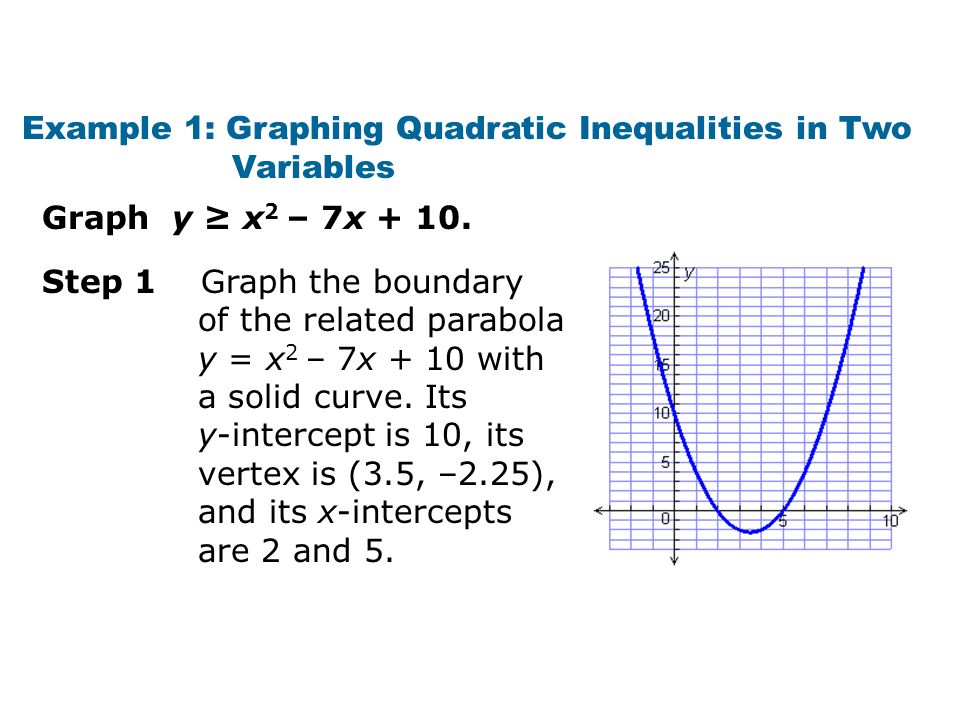



Warm Up 1 Graph The Inequality Y 2x 1 Solve Using Any Method 2 X 2 16x 63 X 2 8x 3 7 Ppt Download



Solution A Convert The Inequality X Y Gt 7 To Slope Intercept Form B Graph The Inequality In The Space Provided At The Right You May Use Any Method To Fine The
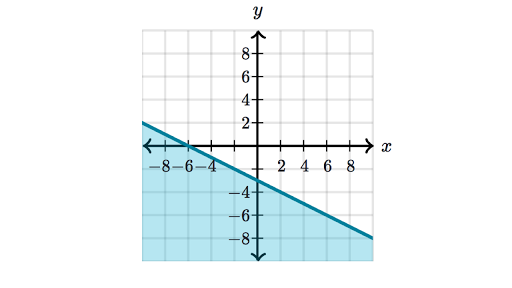



Graphing Inequalities X Y Plane Review Article Khan Academy



2
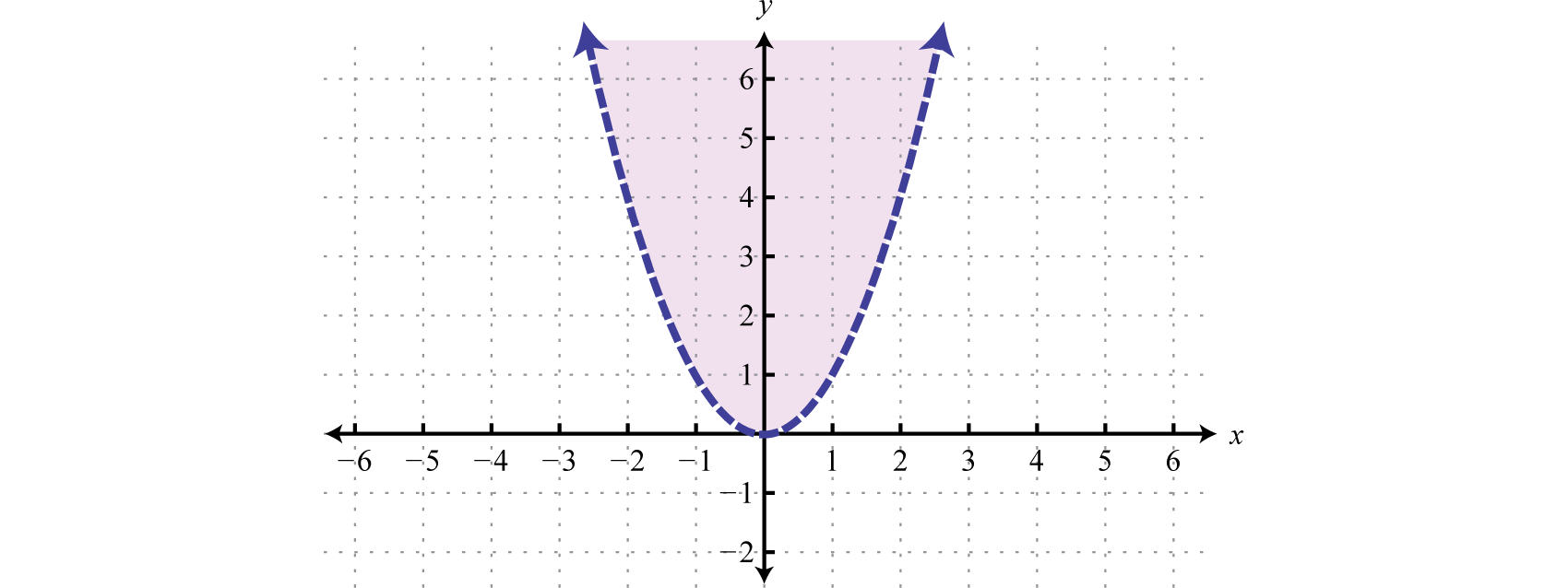



Solving Inequalities With Two Variables




Which Of The Following Shows The Graph Of The Inequality Y Gt X 2 Brainly Com




Which System Of Linear Inequalities Is Represented By The Graph Y Gt X 3 And 3x Y Gt 2 Y Brainly Com
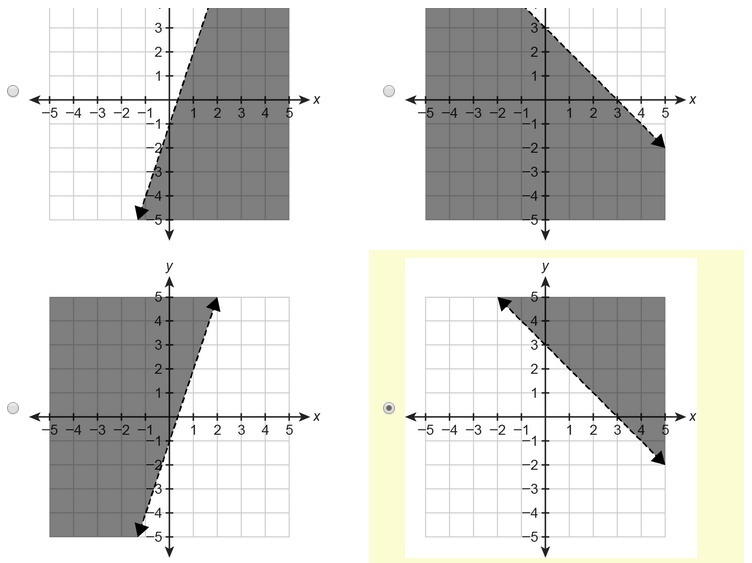



Which Graph Represents The Inequality Y Gt 3 X




The Graph Of Positive Trivial And Nontrivial Solutions Of X Y Y X Download Scientific Diagram



Graphing Systems Of Inequalities



Solution Graph The Inequality Y Lt X 4 This Is Very Difficult Please Help
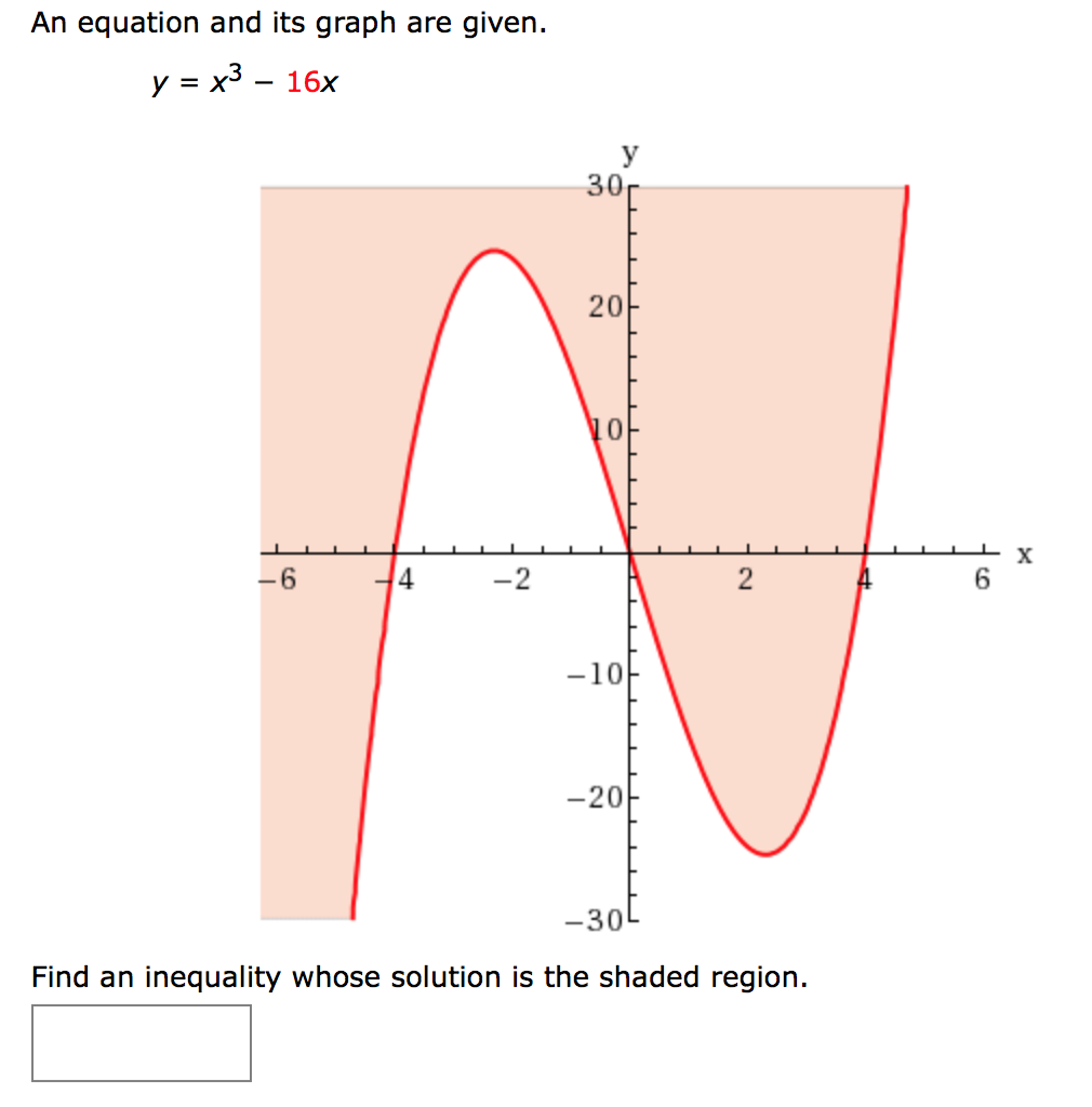



Solved An Equation And Its Graph Are Given Y X 3 16x Chegg Com



Solution Graph Solution Set Of This Linear Inequality X Y Gt 2



Chapter 3 4 Polynomial Functions Y X Graph
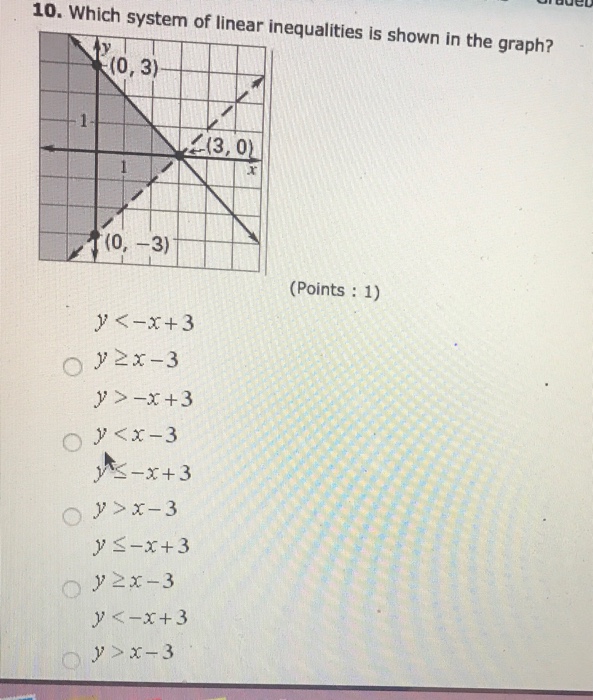



Solved Which System Of Linear Inequalities Is Shown In The Chegg Com




Practice B Linear Inequalities In Two Variables Weeblyasb Bangna Practice B Linear Inequalities In Two Variables Graph Each Inequality 1 Y X 2 2 Y 3x 5 X Y X Y Solve Each Inequality




Solving Systems Of Linear Inequalities Two Variables




Graph The Linear Equation Yx 2 1 Draw
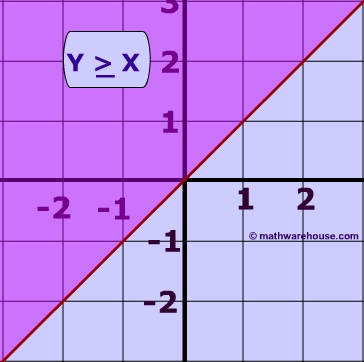



Linear Inequalities How To Graph The Equation Of A Linear Inequality




Ex 6 3 8 Solve X Y 9 Y X X 0 Graphically Ex 6 3
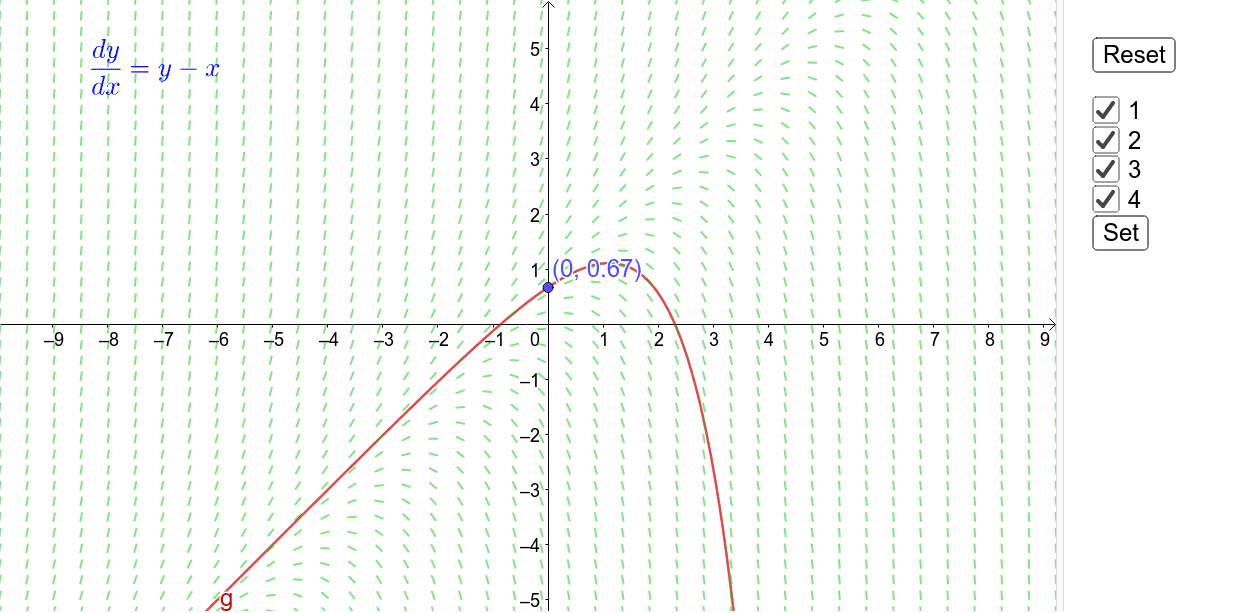



Dy Dx Y X Geogebra



Graphing Systems Of Inequalities
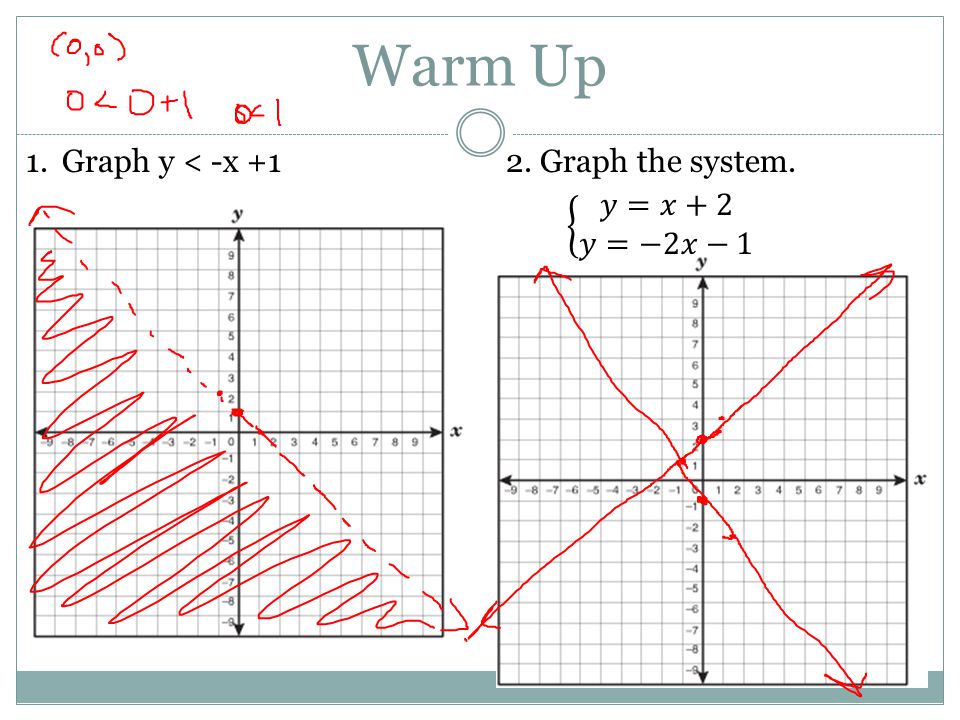



Section 3 4 Systems Of Linear Inequalities Warm Up 1 Graph Y X 12 Graph The System Ppt Download



Graphs Of Linear Inequalities




Which System Of Inequalities Is Represented By The Graph A Y 1y X 0 C Y 1y X 0 Brainly Com



0 件のコメント:
コメントを投稿